Абсолютная деформация сдвига измеряется

Возьмем однородное тело, имеющее форму прямоугольного параллелепипеда, и приложим к его противолежащим граням силы и 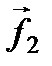(f₁ = f₂ =f), направленные параллельно этим граням (рис. 45). Если действие сил будет равномерно распределено по всей поверхности соответствующей грани S, то в любом сечении, параллельном этим граням, возникнет тангенциальное напряжение

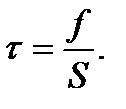(116)

Под действием напряжений тело деформируется таким образом, что верхняя (на рисунке) грань сместится относительно нижней на некоторое расстояние а. Если тело мысленно разбить на элементарные горизонтальные слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев. По этой причине деформация такого вида получила название сдвига.

При деформации сдвига любая прямая, первоначально перпендикулярная к горизонтальным слоям, повернется на некоторый угол φ. Следовательно, отношение сдвига δа двух произвольно взятых слоев к расстоянию между этими слоями δb будет одинаково для любой пары слоев. Это отношение естественно взять в качестве характеристики деформации сдвига:

(117)

Величина γназывается относительным сдвигом. В силу малости угла φ можно положить tgφ = φ. Следовательно, относительный сдвиг γоказывается равным углу сдвига φ. Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению:

(118)

Коэффициент G зависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45° (tgφ = 1), если бы при столь больших деформациях не был превзойден предел упругости.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8657 — | 7435 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Абсолютный сдвиг

Абсолютный сдвиг прямо пропорционален сдвигающей силе, расстоянию между сдвигаемыми гранями и обратно пропорционален площади сечения этих граней и модулю упругости при сдвиге. [1]

Абсолютный сдвиг выражается в мерах длины, а отно-сител ьный сдвиг — в радианах. [2]

Абсолютный сдвиг выражается в мерах длины, а относительный сдвиг-в радианах. Величина у, как показывает огыт, прямо пропорциональна величине касательных напряжений. [3]

Абсолютный сдвиг прямо пропорционален поперечной силе, длине элемента бруса и обратно пропорционален жесткости при сдвиге. Формула эта вполне аналогична формуле для абсолютного удлинения, но является приближенной, так как в действительности напряжение т переменно по высоте сечения. [4]

Абсолютный сдвиг будем считать положительным, если модульная прямая располагается от центра колеса дальше делительной прямой, и отрицательным, если она находится между делительной прямой и центром нарезаемого колеса. [6]

Абсолютный сдвиг определяется линейными перемещениями точек, лежащих в сдвигаемом сечении. Величина абсолютного сдвига зависит от расстояния сдвигаемого сечения до сечения, относительно которого определяется сдвиг. [7]

Величина абсолютного сдвига прямо пропорциональна сдвигающим силам и расстоянию между ними и обратно пропорциональна жесткости поперечного сечения при сдвиге. [8]

T-е-отношение абсолютного сдвига между двумя близкими смежными сечениями к расстоянию между этими сечениями; выражается он в радианах. [9]

Отношение абсолютного сдвига к длине участка, на котором про — В исходит сдвиг, называют относи-с тельным сдвигом. [11]

Деформация абсолютного сдвига измеряется стрелочными индикаторами с ценой деления шкалы — 0 01 мм. [13]

Величина абсолютного сдвига зависит не только от величины касательных напряжений, но и от размеров выделенного элемента. Назовем площадь граней, по которым действуют касательные напряжения, F; расстояние между параллельными гранями обозначено через а ( фиг. [14]

Величина абсолютного сдвига зависит не только от величины касательных напряжений, но и от размеров выделенного элемента. [15]

Если деформация растяжения возникает, когда стержень тянут, а сжатия – когда его сдавливают, то деформация сдвига происходят тогда, когда его пытаются, например, разрезать. Сдвиг и будет темой нашей третье беседы. Вследствие сдвига разрушаются сварные и болтовые соединения, дают течь корабли, шатаются столы и т. п.

Что такое сдвиг? Какие внутренние усилия возникают в поперечных сечениях стержня при сдвиге?

Сдвигом называется такой вид деформации, при котором одна часть стержня смещается относительно другой (как скользят, например, карты в колоде). Деформация сдвига будет происходить, например, в том случае, если к стержню приложить две равные по значению и противоположно направленные силы P, перпендикулярные к его оси z (рис. 3.1, а). Расстояние между этими силами должно быть очень малым, чтобы моментом, создаваемым этими силами, можно было пренебречь.

Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная (перерезывающая) сила .

Далее мы увидим, что деформация сдвига возникает и при кручении стержня.

Что называется абсолютным сдвигом и углом сдвига (относительным сдвигом)?

В результате деформации сдвига одно поперечное сечение стержня смещается (скользит) относительно другого на некоторую величину , называемуюабсолютным сдвигом.

Малый угол , на который изменится первоначальнопрямойугол (рис. 3.1,б), называетсяуглом сдвига или относительным сдвигом.Угол сдвига выражается врадианах.

Какие напряжения возникают в поперечных сечениях стержня при сдвиге?

Как уже отмечалось во введении, мерой скольжения одного поперечного сечения относительно другого являются касательные напряжения.

Будем считать, что касательные напряжения распределены по всей площади поперечного сечения равномерно (рис. 3.2).

Тогда, если в поперечном сечении стержня площадью F возникает перерезывающая сила , то касательные напряжения влюбой точке этого сечения будут равны

.

Касательные напряжения измеряются в тех же единицах, что и нормальные напряжения: мегапаскалях, килоньютонах на квадратный сантиметр (МПа, кН/см 2 ), а также в килограммах силы на квадратный сантиметр или миллиметр (кгс/см 2 , кгс/мм 2 ).

Как записывается закон Гука при сдвиге? Что называется модулем сдвига, в каких единицах он измеряется?

Опытным путем установлено, что в пределах упругой сдвиговой деформации касательные напряжения пропорциональны углу сдвига:

. (3.1)

Соотношение (3.1) представляет собой закон Гука при сдвиге.

Коэффициент пропорциональности G в этой формуле называется модулем сдвига. Видно, что он измеряется в тех же единицах, что и касательное напряжение.

Модуль сдвига G является физической постоянной для материала, характеризующей его жесткость при сдвиге. Значение модуля сдвига G может быть определено экспериментально.

Какая зависимость существует между модулем сдвига и модулем Юнга?

Для изотропных материалов эта зависимость имеет вид:

.

Как уже отмечалось ранее, значение коэффициент Пуассона лежит в пределах.Следовательно,

.

Например, для стали любой марки:

МПа,

что соответствует значению модуля сдвига, получаемому в результате проведения эксперимента на сдвиг (или на кручение).