Формула для пружинного и математического маятника

Сохранение энергии при колебаниях математического маятника

При гармонических колебаниях полная механическая энергия системы сохраняется (остается постоянной).

Полная механическая энергия математического маятника складывается из кинетической энергии и потенциальной энергии:

где W k — кинетическая энергия, W k = = mv 2 /2; W p — потенциальная энергия, W p = mgh ; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия (рис. 10.15).

В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).

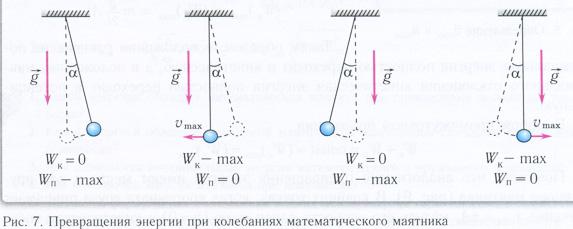
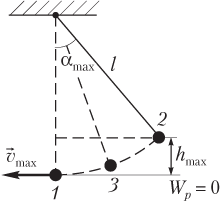
При гармонических колебаниях математический маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию математического маятника в трех положениях (см. рис. 10.15):

1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:

W k max = m v max 2 2 ;

потенциальная энергия равна нулю; полная энергия совпадает с максимальной кинетической энергией:

2) в крайнем положении ( 2 ) тело поднято над исходным уровнем на максимальную высоту h max , поэтому потенциальная энергия также максимальна:

W p max = m g h max ;

кинетическая энергия равна нулю; полная энергия совпадает с максимальной потенциальной энергией:

3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v и поднято над исходным уровнем на некоторую высоту h , поэтому полная энергия представляет собой сумму

E = m v 2 2 + m g h ,

где mv 2 /2 — кинетическая энергия; mgh — потенциальная энергия; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия.

При гармонических колебаниях математического маятника полная механическая энергия сохраняется:

Значения полной энергии математического маятника в трех его положениях отражены в табл. 10.1.

№	Положение	W p	W k	E = W p + W k
1	Равновесие		m v max 2 / 2	m v max 2 / 2
2	Крайнее	mgh max		mgh max
3	Промежуточное (мгновенное)	mgh	mv 2 /2	mv 2 /2 + mgh

Значения полной механической энергии, представленные в последнем столбце табл. 10.1, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :

m v max 2 2 = m g h max ;

m v max 2 2 = m v 2 2 + m g h ;

m g h max = m v 2 2 + m g h ,

где m — масса груза; g — модуль ускорения свободного падения; v — модуль мгновенной скорости груза в положении 3 ; h — высота подъема груза над положением равновесия в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; h max — максимальная высота подъема груза над положением равновесия в положении 2 .

Угол отклонения нити математического маятника от вертикали (рис. 10.15) определяется выражением

cos α = l − h l = 1 − h l ,

где l — длина нити; h — высота подъема груза над положением равновесия.

Максимальный угол отклонения α max определяется максимальной высотой подъема груза над положением равновесия h max :

cos α max = 1 − h max l .

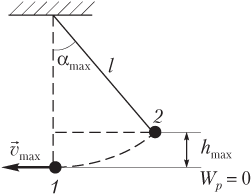
Пример 11. Период малых колебаний математического маятника равен 0,9 с. На какой максимальный угол от вертикали будет отклоняться нить, если, проходя положение равновесия, шарик движется со скоростью, равной 1,5 м/с? Трение в системе отсутствует.

Решение . На рисунке показаны два положения математического маятника:

• положение равновесия 1 (характеризуется максимальной скоростью шарика v max );
• крайнее положение 2 (характеризуется максимальной высотой подъема шарика h max над положением равновесия).

Искомый угол определяется равенством

cos α max = l − h max l = 1 − h max l ,

где l — длина нити маятника.

Максимальную высоту подъема шарика маятника над положением равновесия найдем из закона сохранения полной механической энергии.

Полная энергия маятника в положении равновесия и в крайнем положении определяется следующими формулами:

E 1 = m v max 2 2 ,

где m — масса шарика маятника; v max — модуль скорости шарика в положении равновесия (максимальная скорость), v max = 1,5 м/с;

где g — модуль ускорения свободного падения; h max — максимальная высота подъема шарика над положением равновесия.

Закон сохранения полной механической энергии:

m v max 2 2 = m g h max .

Выразим отсюда максимальную высоту подъема шарика над положением равновесия:

h max = v max 2 2 g .

Длину нити определим из формулы для периода колебаний математического маятника

Подставим h max и l в выражение для косинуса искомого угла:

cos α max = 1 − 2 π 2 v max 2 g 2 T 2

и произведем вычисление с учетом приблизительного равенства π 2 = 10:

cos α max = 1 − 2 ⋅ 10 ⋅ ( 1,5 ) 2 10 2 ⋅ ( 0,9 ) 2 = 0,5 .

Отсюда следует, что максимальный угол отклонения составляет 60°.

Строго говоря, при угле 60° колебания шарика не являются малыми и пользоваться стандартной формулой для периода колебаний математического маятника неправомерно.

Сохранение энергии при колебаниях пружинного маятника

Полная механическая энергия пружинного маятника складывается из кинетической энергии и потенциальной энергии:

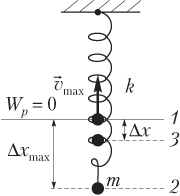
где W k — кинетическая энергия, W k = mv 2 /2; W p — потенциальная энергия, W p = k (Δ x ) 2 /2; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины (рис. 10.16).

В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).

При гармонических колебаниях пружинный маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию пружинного маятника в трех положениях (см. рис. 10.16):

1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:

W k max = m v max 2 2 ;

потенциальная энергия пружины равна нулю, так как пружина не деформирована; полная энергия совпадает с максимальной кинетической энергией:

2) в крайнем положении ( 2 ) пружина имеет максимальную деформацию (Δ x max ), поэтому потенциальная энергия также имеет максимальное значение:

W p max = k ( Δ x max ) 2 2 ;

кинетическая энергия тела равна нулю; полная энергия совпадает с максимальной потенциальной энергией:

3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v , пружина имеет в этот момент некоторую деформацию (Δ x ), поэтому полная энергия представляет собой сумму

E = m v 2 2 + k ( Δ x ) 2 2 ,

где mv 2 /2 — кинетическая энергия; k (Δ x ) 2 /2 — потенциальная энергия; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины.

При смещении груза пружинного маятника от положения равновесия на него действует возвращающая сила , проекция которой на направление движения маятника определяется формулой

где x — смещение груза пружинного маятника от положения равновесия, x = ∆ x , ∆ x — деформация пружины; k — коэффициент жесткости (упругости) пружины маятника.

При гармонических колебаниях пружинного маятника полная механическая энергия сохраняется:

Значения полной энергии пружинного маятника в трех его положениях отражены в табл. 10.2.

№	Положение	W p	W k	E = W p + W k
1	Равновесие		m v max 2 / 2	m v max 2 / 2
2	Крайнее	k (Δ x max ) 2 /2		k (Δ x max ) 2 /2
3	Промежуточное (мгновенное)	k (Δ x ) 2 /2	mv 2 /2	mv 2 /2 + k (Δ x ) 2 /2

Значения полной механической энергии, представленные в последнем столбце таблицы, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :

m v max 2 2 = k ( Δ x max ) 2 2 ;

m v max 2 2 = m v 2 2 + k ( Δ x ) 2 2 ;

k ( Δ x max ) 2 2 = m v 2 2 + k ( Δ x ) 2 2 ,

где m — масса груза; v — модуль мгновенной скорости груза в положении 3 ; Δ x — деформация (растяжение или сжатие) пружины в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; Δ x max — максимальная деформация (растяжение или сжатие) пружины в положении 2 .

Пример 12. Пружинный маятник совершает гармонические колебания. Во сколько раз его кинетическая энергия больше потенциальной в тот момент, когда смещение тела из положения равновесия составляет четверть амплитуды?

Решение . Сравним два положения пружинного маятника:

• крайнее положение 1 (характеризуется максимальным смещением груза маятника от положения равновесия x max );
• промежуточное положение 2 (характеризуется промежуточными значениями смещения от положения равновесия x и скорости v → ).

Полная энергия маятника в крайнем и промежуточном положениях определяется следующими формулами:

E 1 = k ( Δ x max ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆ x max — амплитуда колебаний (максимальное смещение от положения равновесия), ∆ x max = A ;

• в промежуточном положении —

E 2 = k ( Δ x ) 2 2 + m v 2 2 ,

где m — масса груза маятника; ∆ x — смещение груза от положения равновесия, ∆ x = A /4.

Закон сохранения полной механической энергии для пружинного маятника имеет следующий вид:

k ( Δ x max ) 2 2 = k ( Δ x ) 2 2 + m v 2 2 .

Разделим обе части записанного равенства на k (∆ x ) 2 /2:

( Δ x max Δ x ) 2 = 1 + m v 2 2 ⋅ 2 k Δ x 2 = 1 + W k W p ,

где W k — кинетическая энергия маятника в промежуточном положении, W k = mv 2 /2; W p — потенциальная энергия маятника в промежуточном положении, W p = k (∆ x ) 2 /2.

Выразим из уравнения искомое отношение энергий:

W k W p = ( Δ x max Δ x ) 2 − 1

и рассчитаем его значение:

W k W p = ( A A / 4 ) 2 − 1 = 16 − 1 = 15 .

В указанный момент времени отношение кинетической и потенциальной энергий маятника равно 15.

Урок 38. Подготовка к ЕГЭ по физике. Часть 1. Механика.

Конспект урока "Математический и пружинный маятники"

В данной теме разговор пойдёт о математическом и пружинном маятниках и их важных характеристиках.

Рассмотрим для начала математический маятник. Математическим маятником называется находящаяся в гравитационном поле материальная точка, подвешенная на невесомой и нерастяжимой нити, прикрепленной к подвесу. Математический маятник — это модель малых реальных колебаний тела под действием силы тяготения при условии, что можно пренебречь:

1) размерами подвешенного тела, по сравнению с длиной нити;

2) сопротивлением движению тела;

3) массой нити и ее деформацией.

Рассмотрим подробно колебания математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса движется прямолинейно и равномерно или же покоится. И так, пусть в начальный момент времени маятник покоится в положении равновесия. Тогда, действующие на маятник сила упругости нити и сила тяжести материальной точки взаимно компенсируются.

Теперь отклоним маятник на некоторое расстояние от точки равновесия и отпустим его. В этом случае, сила тяжести и сила упругости нити уже не будут компенсировать друг друга. Разложим вектор силы тяжести на две составляющих — тангенциальную и нормальную.

Как видим, тангенциальная составляющая силы тяжести направлена к положению равновесия, то есть она является возвращающей силой. При этом она сообщает материальной точке тангенциальное ускорение и маятник начнет двигаться к положению равновесия с возрастающей по модулю скоростью. А нормальная составляющая силы тяжести, как видно из рисунка, направлена вдоль нити против силы упругости. Их равнодействующая сообщает маятнику нормальное ускорение, которое изменяет направление вектора скорости. В результате маятник начинает двигаться по дуге.

Чем ближе маятник будет подходить к положению равновесия, тем меньше становиться значение возвращающей силы и тем больше становиться скорость движения маятника. Дойдя до положения равновесия, возвращающая сила становится равной нулю.

При этом скорость движения маятника достигает своего максимума и, не останавливаясь, маятник продолжает свое движение дальше уже по инерции, поднимаясь по дуге вверх. При этом вновь возникает возвращающая сила, которая становится тем больше, чем выше поднимается маятник. Но так как возвращающая сила теперь направлена против движения маятника, то его скорость убывает и в точке D скорость маятника становится равной нулю.

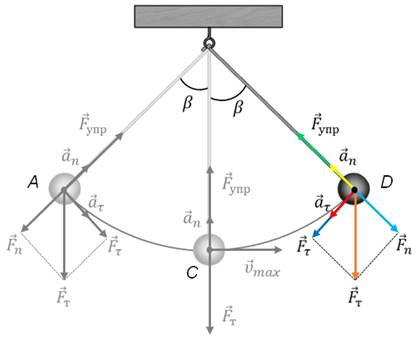
Маятник на мгновение останавливается, а затем начинает двигаться в обратном направлении к положению равновесия. Опять пройдя его по инерции, маятник, замедляя свое движение, дойдет до точки А, тем самым совершив одно полное колебание. А так как силы сопротивления отсутствуют, то после этого движение маятника будет повторяться в уже описанной последовательности.

Получим уравнение, описывающее свободные колебания математического маятника. Пусть маятник в данный момент времени находится в точке B.

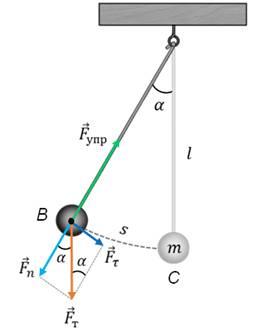
Его смещение от положения равновесия в этот момент равно длине дуги CB.

Пусть длина нити подвеса маятника равна l, а его масса m. Из рисунка видно, что значение возвращающей силы (то есть тангенциальной составляющей силы тяжести), можно найти как произведение модуля силы тяжести на синус угла отклонения маятника от вертикали.

Из геометрии известно, что по определению синус острого угла есть отношение противолежащего катета к гипотенузе. Также из геометрии известно, что при малых углах (то есть когда острый угол меньше десяти градусов) синус угла можно заменить его градусной мерой.

Перепишем уравнение для тангенциальной составляющей силы тяжести с учетом последнего равенства.

Обратите внимание на знак «минус» в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия. Теперь применим второй закон Ньютона для нашего маятника, в проекциях на направление касательной к траектории движения математического маятника.

Таким образом, имеются два уравнения, в которых равны их левые части. А раз равны левые, то и правые части этих равенств также должны быть равными. Сократив полученное равенство на массу маятника, приходим к тому, что тангенциальное ускорение математического маятника прямо пропорционально его смещению и направлено к положению равновесия.

Эту формулу называют динамическим уравнением движения математического маятника.

Теперь перепишем это уравнение следующим образом

А теперь сравним его с уравнением гармонических колебаний.

Из такой записи видно, что колебания математического маятника являются гармоническими. А так как рассмотренные колебания происходили только под действием внутренних сил, то это были свободные колебания. Таким образом, можно сделать важный вывод о том, что при малых углах отклонения свободные колебания математического маятника являются гармоническими.

Также из анализа формул следует, что циклическая частота колебаний маятника равна квадратному корню из отношения ускорения свободного падения к длине маятника.

Помня о том, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний математического маятника.

Полученная формула называется формулой Гюйгенса, так впервые была получена нидерландским физиком Христианом Гюйгенсом.

Следует обратить внимание на то, что эту формулу можно использовать для расчета периода при выполнении одновременно двух условий:

1) колебания маятника должны быть малыми, так как эта формула дает результаты приемлемой точности (ошибка менее одного процента) при углах, не превышающих 4º;

2) точка подвеса маятника должна покоиться или двигаться прямолинейно и равномерно относительно инерциальной системы отсчета, в которой находится маятник.

Дело в том, что если точка подвеса математического маятника движется с некоторым ускорением, то изменяется сила натяжения нити. Это приводит к изменению возвращающей силы, а, следовательно, частоты и периода колебаний. В этом случае в формуле периода математического маятника ускорение свободного падения следует заменить на так называемое «эффективное» ускорение маятника в неинерциальной системе отсчета.

«Эффективное» ускорение можно найти, как векторную сумму ускорения свободного падения и вектора, противоположного вектору ускорения, с которым движется маятник.

Теперь рассмотрим колебания пружинного маятника. Пружинным маятником называется система, состоящая из пружины жесткостью k и материальной точки массой m.

В простейшей модели пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают:

1) любыми силами сопротивления;

2) размерами тела, то есть тело принимают за материальную точку;

3) массой пружины.

Различают два вида пружинных маятников — горизонтальный и вертикальный.

В горизонтальном пружинном маятнике, колебания тела происходят вдоль горизонтальной прямой.

У вертикального пружинного маятника колебания происходят вдоль вертикальной прямой.

Рассмотрим более подробно колебания идеального горизонтального пружинного маятника. Пусть в начальный момент времени пружина не деформирована, и тело находится в положении равновесия.

Теперь выведем тело из положения равновесия, например, сжав пружину на некоторую величину, и отпустим его. И так, со стороны деформированной пружины на тело начнет действовать сила упругости, которая всегда будет направленна к положению равновесия, и под действием этой силы тело начнет ускоренно двигаться. При этом в самом крайнем положении на тело действует максимальная сила упругости, так как здесь абсолютное удлинение пружины наибольшее. Значит и ускорение тела в этом положении максимальное.

При движении тела к положению равновесия абсолютное удлинение пружины начинает уменьшаться, а, следовательно, уменьшается и ускорение, сообщаемое силой упругости. Но так как ускорение сонаправлено со скоростью, то скорость маятника увеличивается и в положении равновесия, как и в случае с математическим маятником, она будет максимальна.

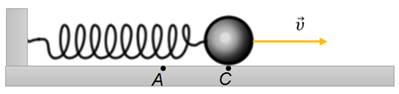
Достигнув положения равновесия, тело не остановится (хотя в этом положении пружина не деформирована), а будет по инерции двигаться дальше, растягивая пружину. Возникающая при этом сила упругости направлена теперь против движения тела и тормозит его. В точке D тело на мгновение остановится, так как его скорость окажется равной нулю. Но ускорение в этой точке максимально, так как максимальна действующая сила упругости и под действием этой силы тело начнет двигаться в обратную сторону, к положению равновесия.

Вновь пройдя его по инерции, тело, сжимая пружину и замедляя движение, дойдет до точки A, то есть совершит одно полное колебание. После этого движение маятника будет повторяться в описанной последовательности.

Таким образом, причинами свободных колебаний пружинного маятника являются действие силы упругости, возникающей при деформации пружины, и инертность тела.

Получим уравнение, описывающее движение пружинного маятника. И так, согласно второму закону Ньютона, единственный результат действия силы упругости — это сообщение телу ускорения.

По закону Гука, сила упругости прямо пропорциональна смещению тела и противоположно ему направлена.

Перепишем второй закон Ньютона с учетом определения силы упругости пружины.

Как видно из уравнения, ускорение маятника прямо пропорционально смещению и противоположно ему по направлению.

Перепишем уравнение следующим образом

Полученное равенство является динамическим уравнением движения пружинного маятника.

Сравнивая его с уравнением гармонических колебаний, видим, что пружинный маятник совершает гармонические колебания с циклической частотой равной

Учитывая, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний пружинного маятника.

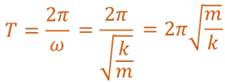
По этой же формуле можно рассчитывать и период колебаний вертикального пружинного маятника.

Рассмотрели математический и пружинный маятники. Рассмотрели условия возникновения свободных гармонических колебаний в таких системах. А также вспомнили формулы, по которым можно рассчитать период свободных колебаний математического и пружинного маятников.

Разделы: Физика

Класс: 9

На уроке хотелось бы сразу дать учащимся в сравнении колебания пружинного и математического маятников. Обратить внимание на сходство процессов, одинаковое изменение энергий (кинетической и потенциальной) через одинаковые промежутки времени.

Пояснение по форме объяснения учебного материала: на доске удобнее расположить рисунки маятников рядом, разделив доску пополам. Записи для описания характеристик маятников делать на одном уровне.

Цели урока:

1. Ввести понятия колебательных систем,
2. Рассмотреть на примерах математического и пружинного маятников особенность свободных колебаний.
3. Определение параметров идеальных колебательных систем.
4. Научить выделять существенные признаки колебательных систем.
5. Формирование потребности в новых знаниях, усвоение предмета.

Демонстрации:

1. Математический маятник.
2. Пружинный маятник.

Ход урока

I. Организационный момент (2 мин.)

II. Проверка домашнего задания (7 мин.)

Двое учащихся у доски решают по задаче (проверка и закрепление домашнего материала):

1. За какое время маятник совершит 30 колебаний, если период колебаний 0,5 с? Чему равна частота колебаний?
2. Период колебаний крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Какое насекомое сделает больше взмахов крыльями за одну минуту и на сколько?

Пока ребята решают задачи у доски, в классе проводится фронтальный опрос:

1. Что такое колебания?
2. Приведите примеры колебаний в природе и технике.
3. Что такое период колебаний? Единицы измерения?
4. Что такое частота колебаний? Единицы измерения?
5. Что такое амплитуда колебаний?

Проверяем и списываем задачи с доски, корректируем по форме записи и решению.

III. Объяснение нового материала (25 мин.)

Демонстрация колебательных процессов нитяного и пружинного маятника.

Если вывести системы из положения равновесия, то можем заметить, что через некоторое время колебания затухают. Почему колебания стали возможны?

При выведении систем из положения равновесия, им передается запас энергии, благодаря чему возникают колебания. Энергия заканчивается, система останавливается.

Такие колебания, происходящие только благодаря начальному запасу энергии, называются свободными колебаниями.

Тогда, тело, прикрепленное к пружине, и грузик, подвешенный на нити, называют колебательными системами.

Или физическую систему (тело), в которой при отклонении от положения равновесия возникают и существуют колебания, называют колебательной системой.

Маятники: нитяной и пружинный можно отнести к колебательным системам.

Но, для определения основных характеристик, определяемых для колебательных систем, будем считать, что за небольшой промежуток времени потери энергии при колебательном движении достаточно малы, им можно пренебречь. Тогда эти системы можно считать идеальными.

Рассмотрим, что математический и пружинный маятники – это идеальные модели колебательных систем, в которых не действуют силы трения. Такие системы обладают, как любое физическое тело, обладают механической энергией.

(На доске удобнее расположить рисунки маятников рядом, разделив доску пополам. Сравнение положений маятников, характеристик колебательных процессов в сравнении).

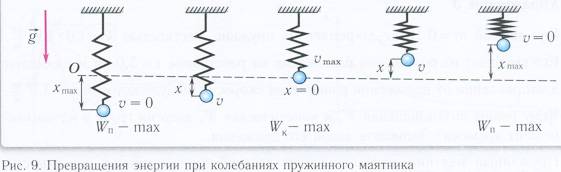
Пружинный маятник

Пружинный маятник – это колебательная система, состоящая из материальной точки массой m и пружин,при движении которой не действуют силы трения.

Период колебаний пружинного маятника можно найти по формуле

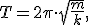
где k – коэффициент жесткости пружины маятника. Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды колебаний (в пределах выполнимости закона Гука).

Энергия колебаний пружинного маятника:

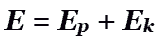– Энергия колебаний – это сумма потенциальной энергии пружины и кинетической энергии груза.

Формулы потенциальной и кинетической энергий:

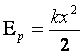
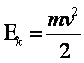
Рассмотрим поведение маятника и изменение его энергии в различных положениях:

1 – (крайнее верхнее положение), х – смещение max, v – скорость равна 0,

от х зависит потенциальная энергия, следовательно Е max, а кинетическая энергия связана со скоростью v, следовательно Е=0.

Переход из 1-2 сопровождается изменением следующих величин:

х – уменьшается, Е уменьшается, v – увеличивается, Е – увеличивается.

2 – (тело проходит положение равновесия)

v – скорость при прохождении положения равновесия самая большая, v – max, следовательно Е – max.

Переход из положения 2-3 происходит при увеличении х, то потенциальна энергия увеличивается, а v- скорость уменьшается, следовательно и кинетическая энергия тоже уменьшается.

3 – (крайне правое положение тела)

х – смещение max, v – скорость равна 0, следовательно Е max, а кинетическая энергия следовательно Е =0.

Математический маятник.

Рассмотрим простой маятник – шарик, подвешенный на длинной прочной нити. Такой маятник называется физический.

Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь. Растяжением нити также можно пренебречь, так как оно очень мало. Если масса нити во много раз меньше массы шарика, то массой нити также можно пренебречь. В этом случае

мы получаем модель маятника, которая называется математическим маятником.

Математическим маятником называется, материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле силы тяжести (или других сил)

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:

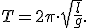
Энергия колебаний пружинного маятника:

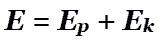– Энергия колебаний – это сумма потенциальной энергии пружины и кинетической энергии груза.

Формулы потенциальной и кинетической энергий:

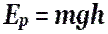
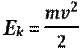
IV. Обобщение материала. (6 мин.)

Тела могут совершать периодически повторяющиеся движения около неподвижной точки. При этом меняются параметры колебательной системы: положение тела. Его скорость, кинетическая и потенциальная энергия.

Приведите свои примеры колебательного движения.

Учащиеся могут привести примеры колеблющихся тел из окружающей жизни.

V. Домашнее задание (2 мин.)

П. 25, 26 упр. 23(1), упр 24(2)

Литература:

1. Перышкин А.В., Гутник Е.М. Физика.9кл.: Учеб. для общеобразоват. учеб. заведений. – М.: Дрофа, 2009.
2. А.В. Перышкин. сборник задач по физике: 7-9кл. – М.: Издательство «Экзамен», 2006.