Как влияет природа материала на модуль юнга

Упругие свойства материалов и методы их определения. Связь между упругими константами.

свойство тел восстанавливать свою первоначальную форму и объем когда действие силы прекращается называется упругостью.

Упругие свойства некоторых материалов E и G – модули Юнга и сдвига; μ – коэффициент Пуассона; K – модуль всестороннего сжатия

Модулем сдвига – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям.(Па)

Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса (в ньютонах на метр в квадрате или в паскалях).
Коэффициент Пуассона — абсолютная величина отношения поперечной и продольной относительной деформации образца материала. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец.

Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении).

Методы определения упругих свойств:
1 статические использования на растяжение, влияют остаточные напряжения.
2 Резонансный метод
3 Звуковой методами
4 Рентгеновский

Связь между упругими константами
модуль нормальной упругости (Гука)
модуль сдвига (касательная упругость)
модуль объёмной упругости
Величина модуля определяет жесткость материалов и характеризуется силой смещения атомов из положения равновесия.

Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона диаграммы напряжений-деформаций:

1. λ (лямбда) — модуль упругости;

2. p — напряжение, вызываемое в образце действующей силой (равно силе, делённой на площадь приложения силы);

3. упругая деформация образца, вызванная напряжением (равна отношению изменения размера образца после деформации к его первоначальному размеру).

Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения λ также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:

Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия(удлинения). Часто модуль Юнга называют просто модулем упругости.

Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения).

Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия.

Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.

Дата добавления: 2015-07-13 ; Просмотров: 1185 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.

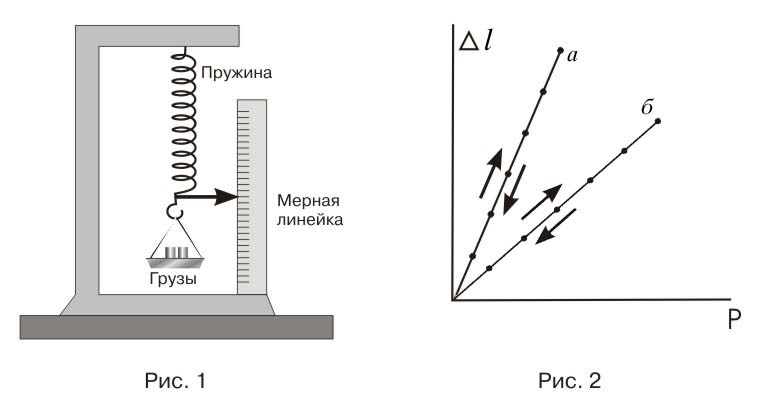
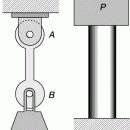
При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение D l, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.

Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.3). Эти графики называются характеристиками пружины.

Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины D l = P / C

Жесткость пружины С имеет размерность кг / смup122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.

В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.

Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.

При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.

Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос. Эти примеры доказывают, что проявление упругих свойств было давно известно и давно использовалось людьми. Но понимание того, что любое твердое тело под действием даже небольших нагрузок обязательно деформируется, хотя и на очень малую величину, впервые появилось в 1660 у Роберта Гука, современника и коллеги великого Ньютона. Гук был выдающимся ученым, инженером и архитектором. В 1676 он сформулировал свое открытие очень кратко, в виде латинского афоризма: «Ut tensio sic vis», смысл которого состоит в том, что «какова сила, таково и удлинение». Но опубликовал Гук не этот тезис, а только его анаграмму: «ceiiinosssttuu». (Таким образом тогда обеспечивали приоритет, не раскрывая сути открытия.)

Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т.п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.

Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение D l разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e .

Теперь закон Гука о пропорциональности можно записать в виде:

Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.

Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.

В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.

Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:

Сталь	20·10 4
Медь	10·10 4
Алюминий	7·10 4
Стекло	7·10 4
Кость	3·10 4
Дерево	1·10 4
Резина *	0,001·10 4

Физическая природа упругости связана с электромагнитным взаимодействием (в том числе с силами Ван-дер-Ваальса в решетке кристалла). Можно считать, что упругие деформации связаны с изменением расстояния между атомами.

Упругий стержень имеет еще одно фундаментальное свойство – утоньшаться при растяжении. То, что канаты при растяжении становятся тоньше, было известно давно, но специально поставленные опыты показали, что при растяжении упругого стержня всегда имеет место закономерность: если измерить поперечную деформацию e ‘, т.е. уменьшение ширины стержня d b , деленное на первоначальную ширину b, т.е.

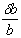
и разделить ее на продольную деформацию e , то это отношение остается постоянным при всех значениях растягивающей силы P, то есть

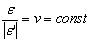
(Полагают, что e ‘ s , что приводит к деформациям, которые задаются тензором e .

В общем случае закон Гука устанавливает связь между компонентами этих тензоров, которую можно записать в виде:

В последние три уравнения входит величина G, которая называется модулем сдвига и выражается через E и v по формуле:

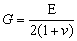
Модуль сдвига можно непосредственно определить из опыта на кручение круглого образца.

В физике для идеального газа вводится уравнение состояния (уравнение Клапейрона – Менделеева). Можно сказать, что закон Гука – это уравнение состояния для идеально упругого тела.

Ильюшин А.А., Ленский В.С. Сопротивление материалов. М., Физматгиз, 1959
Гордон Дж. Почему мы не проваливаемся сквозь пол? М., Мир, 1971
Безухов Н.И. Основы теории упругости, пластичности и ползучести. М., Высшая школа, 1981

Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:

E = def d σ d ε <displaystyle E <stackrel < ext><=>> <frac >>

• E — модуль упругости;
• σ <displaystyle sigma >— напряжение, вызываемое в образце действующей силой (равно силе, делённой на площадь приложения силы);
• ε <displaystyle varepsilon >— упругая деформация образца, вызванная напряжением (равна отношению изменения размера образца после деформации к его первоначальному размеру).

В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):

E = σ ε <displaystyle E=<frac <sigma ><varepsilon >>> .

Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:

• Модуль Юнга ( E ) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
• Модуль сдвига или модуль жесткости ( G или μ <displaystyle mu >) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
• Модуль объёмной упругости или Модуль объёмного сжатия ( K ) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).

Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.

В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.

Формулы преобразования
Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам:
( λ , G ) <displaystyle (lambda ,,G)>	( E , G ) <displaystyle (E,,G)>	( K , λ ) <displaystyle (K,,lambda )>	( K , G ) <displaystyle (K,,G)>	( λ , ν ) <displaystyle (lambda ,, u )>	( G , ν ) <displaystyle (G,, u )>	( E , ν ) <displaystyle (E,, u )>	( K , ν ) <displaystyle (K,, u )>	( K , E ) <displaystyle (K,,E)>
K = <displaystyle K=> модуль объемной

λ + 2 G 3 <displaystyle lambda +<frac <2G><3>>> E G 3 ( 3 G − E ) <displaystyle <frac <3(3G-E)>>> λ 1 + ν 3 ν <displaystyle lambda <frac <1+
u ><3
u >>> 2 G ( 1 + ν ) 3 ( 1 − 2 ν ) <displaystyle <frac <2G(1+
u )><3(1-2
u )>>> E 3 ( 1 − 2 ν ) <displaystyle <frac <3(1-2
u )>>> E = <displaystyle E=> модуль продольной

G 3 λ + 2 G λ + G <displaystyle G<frac <3lambda +2G><lambda +G>>> 9 K K − λ 3 K − λ <displaystyle 9K<frac <3K-lambda >>> 9 K G 3 K + G <displaystyle <frac <9KG><3K+G>>> λ ( 1 + ν ) ( 1 − 2 ν ) ν <displaystyle <frac <lambda (1+
u )(1-2
u )><
u >>> 2 G ( 1 + ν ) <displaystyle 2G(1+
u )> 3 K ( 1 − 2 ν ) <displaystyle 3K(1-2
u )> λ = <displaystyle lambda => первый параметр Ламе G E − 2 G 3 G − E <displaystyle G<frac <3G-E>>> K − 2 G 3 <displaystyle K-<frac <2G><3>>> 2 G ν 1 − 2 ν <displaystyle <frac <2G
u ><1-2
u >>> E ν ( 1 + ν ) ( 1 − 2 ν ) <displaystyle <frac <(1+
u )(1-2
u )>>> 3 K ν 1 + ν <displaystyle <frac <3K
u ><1+
u >>> 3 K ( 3 K − E ) 9 K − E <displaystyle <frac <3K(3K-E)><9K-E>>> G = <displaystyle G=> модуль сдвига

или второй параметр Ламе

3 K − λ 2 <displaystyle 3<frac <2>>> λ 1 − 2 ν 2 ν <displaystyle lambda <frac <1-2
u ><2
u >>> E 2 + 2 ν <displaystyle <frac <2+2
u >>> 3 K 1 − 2 ν 2 + 2 ν <displaystyle 3K<frac <1-2
u ><2+2
u >>> 3 K E 9 K − E <displaystyle <frac <3KE><9K-E>>> ν = <displaystyle
u => коэф. пуассона λ 2 ( λ + G ) <displaystyle <frac <lambda ><2(lambda +G)>>> E 2 G − 1 <displaystyle <frac <2G>>-1> λ 3 K − λ <displaystyle <frac <lambda ><3K-lambda >>> 3 K − 2 G 2 ( 3 K + G ) <displaystyle <frac <3K-2G><2(3K+G)>>> 3 K − E 6 K <displaystyle <frac <3K-E><6K>>> M = <displaystyle M=> λ + 2 G <displaystyle lambda +2G> G 4 G − E 3 G − E <displaystyle G<frac <4G-E><3G-E>>> 3 K − 2 λ <displaystyle 3K-2lambda > K + 4 G 3 <displaystyle K+<frac <4G><3>>> λ 1 − ν ν <displaystyle lambda <frac <1-
u ><
u >>> G 2 − 2 ν 1 − 2 ν <displaystyle G<frac <2-2
u ><1-2
u >>> E 1 − ν ( 1 + ν ) ( 1 − 2 ν ) <displaystyle E<frac <1-
u ><(1+
u )(1-2
u )>>> 3 K 1 − ν 1 + ν <displaystyle 3K<frac <1-
u ><1+
u >>> 3 K 3 K + E 9 K − E <displaystyle 3K<frac <3K+E><9K-E>>>

Модули упругости (Е) для некоторых веществ: