Период колебаний пружинного маятника это

Существуют две простые колебательные системы, которые решены и рассматриваются в школьной программе, — это пружинный и математический маятник. Рассмотрим каждую из них:

1. Пружинный маятник

Пружинным маятником называется система, состоящая из тела массы и пружины, жёсткостью (рис. 1).

Рис. 1. Пружинный маятник

Для такой системы выведены следующие соотношения:

• где

• — собственная частота колебаний системы

Также можем ввести период такого маятника:

• где

• — период колебаний пружинного маятника.

2. Математический маятник

Рис. 2. Математический маятник

Математическим маятником называется малое тело (материальная точка) массы , подвешенная на нити длиной .

Для такой системы выведены следующие соотношения:

• где

• — собственная частота колебаний системы

Также можем ввести период такого маятника:

• где

• — период колебаний пружинного маятника.

Вывод: реальные колебательные системы в курсе школьной физики представлены только пружинным и математическим маятником, которые описываются соотношениями (1) — (4). Достаточно определить необходимый параметр и решить систему.

Рассмотрим простейшую систему, в которой возможна реализация механических колебаний. Допустим, что на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$. Груз движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Массу пружины считаем малой в сравнении с массой груза.

Уравнение движения груза при таких колебаниях имеет вид:

где $<omega >^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

где $<omega >_0=sqrt<frac>>0$- циклическая частота колебаний маятника, $A$ и $B$ — амплитуда колебаний; $<(omega >_0t+varphi )$ — фаза колебаний; $varphi $ и $<varphi >_1$ — начальные фазы колебаний.

Частота и период колебаний пружинного маятника

Косинус (синус) — периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($
u $):

Период связан с циклической частотой колебаний как:

Зная, что для пружинного маятника $<omega >_0=sqrt<frac>$, период колебаний его определим как:

Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:

Примеры задач на период колебания пружинного маятника

Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?

Решение. Сделаем рисунок.

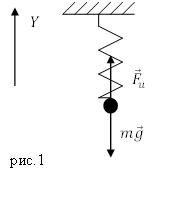
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:

Запишем проекцию уравнения (1.1) на ось Y:

Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:

[F_u=kDelta x left(1.3
ight).]

Используя выражения (1.2) и (1.3) найдем отношение $frac$:

Период колебаний пружинного маятника при малых колебаниях можно найти, используя выражение:

Заменяя отношение массы груза к жесткости пружины на правую часть выражения (1.4), получим:

Вычислим период колебаний нашего маятника, если $g=9,8 frac<м><с^2>$:

Ответ. $T$=0,6 с

Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.

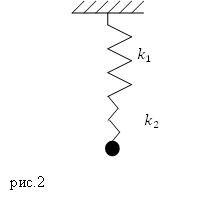
Решение.Период колебаний пружинного маятника равен:

Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:

Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:

Содержание

Маятники

Физическую систему (тело), в которой при отклонении от положения равновесия возникают и существуют колебания, называют колебательной системой.

Рассмотрим простейшие механические колебательные системы: пружинный и математический маятники.

Пружинный маятник

• Пружинный маятник — это колебательная система, состоящая из материальной точки массой m и пружины.

Различают горизонтальный пружинный маятник (рис. 1, а) и вертикальный (рис. 1, б).

Период колебаний пружинного маятника можно найти по формуле

где k — коэффициент жесткости пружины маятника. Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды колебаний (в пределах выполнимости закона Гука).

• Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов ίσος — равный и χρόνος —время).

Математический маятник

Рассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Такой маятник называется физический.

Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Если масса нити во много раз меньше массы шарика, то массой нити также можно пренебречь. В этом случае мы получаем модель маятника, которая называется математическим маятником.

• Математическим маятником называется, материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле силы тяжести (или других сил) (рис. 2).

Mex-majat-03.swf Рис. 2.

Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален (sqrt).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:

При углах отклонения математического маятника α *Вывод формул

*Пружинный маятник

На груз m горизонтального пружинного маятника действуют сила тяжести (m⋅g), сила реакции опоры (N) и сила упругости пружины (F_ynp) (рис. 3, первый две силы на рис. а не указаны). Запишем второй закон Ньютона для случая, изображенного на рис. 3, б

mex-majat-05.swf а (материал с сайта science.up-life.ru)

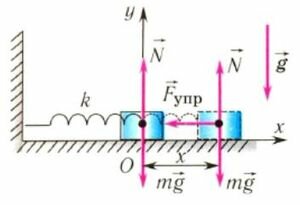
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора

Сравнивая полученное выражение с уравнением гармонических колебаний

находим циклическую частоту колебаний пружинного маятника

Тогда период колебаний пружинного маятника будет равен:

*Математический маятник

На груз m математического маятника действуют сила тяжести (m⋅g) и сила упругости нити (F_ynp) (сила натяжения) (рис. 4). Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для случая, изображенного на рис. 4, б

mex-majat-04.swf а (материал с сайта science.up-life.ru)

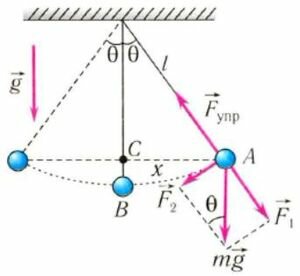
Пусть x — длина дуги AB, следовательно, x = l⋅θ, где угол θ выражен в радианах. Заметим, что при малых углах θ

Сравнивая полученное выражение с уравнением гармонических колебаний

находим, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой

Тогда период колебаний маятника будет равен: