Геометрические размеры зубчатых колес

Задача состоит в том, чтобы по заданному модулю m и числам зубьев z₁, z₂, …, z₆ определить геометрические параметры нулевых эвольвентных зубчатых колёс передаточного механизма (рис.1.4).

Эвольвентные профили зубьев удовлетворяют основному условию синтеза зубчатого зацепления – получению заданного передаточного отношения. Выполнение условия синтеза зависит в первую очередь от размеров зубьев. Эти размеры удобно задавать в долях модуля. Все размеры зубчатого колеса пропорциональны модулю и определяются по следующим формулам:

высота головки зуба h_a = m; (1.33)

высота ножки зуба h_f =1,25 m; (1.34)

высота зуба h =2,25 m; (1.35)

диаметр делительной окружности d = mz; (1.36)

диаметр окружности вершин зубьев d_a = m(z 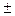2); (1.37)

диаметр окружности впадин зубьев d_f = m(z 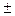2,5); (1.38)

угловой шаг зацепления t = 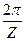; (1.39)

окружной шаг зацепления p = pm ; (1.40)

толщина зуба по делительной окружности s =0,5pm ; (1.41)

межосевое расстояние a =0,5m(z₁ 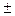z₂). (1.42)

Рис. 1.4. К определению геометрических размеров зубчатого колеса.

В зависимостях (1.37), (1.42) знак плюс относится к внешнему зацеплению, а минус – к внутреннему. В зависимости (1.38) знак минус относится к внешнему зацеплению, а плюс – к внутреннему. По полученным данным определяются качественные показатели зацепления:

а) коэффициент перекрытия пары зубчатых колёс z₁ и z₂;

б) коэффициент полезного действия планетарной ступени и всего механизма передач;

в) мощность, потребляемая машинным агрегатом.

Формулы, по которым определяются данные показатели, приведены в следующем разделе.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8623 — | 7077 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Читайте также:

1. Административные параметры.
2. Аксиологические параметры бытия человека в мире. Экзистенциальный опыт личности.
3. Биологическое здоровье. Уровень физ состояния, его параметры и комплексная оценка
4. Биологическое здоровье. Уровень физ состояния, его параметры и комплексная оценка
5. Биологическое здоровье. Уровень физ состояния, его параметры и комплексная оценка
6. Биполярные транзисторы. Принцип действия, статические и динамические параметры транзисторов.
7. БУКСА КОЛЕСНОЙ ПАРЫ
8. Ванна для проверки колес КС-013
9. Ввести параметры для решения ЗЛП
10. Ввод размеров колеса.
11. Виды освидетельствования колесных пар
12. Виды фотошаблонов. Фоторезисты. Параметры, характеризующие фоторезист.

Геометрические параметры прямозубых цилиндрических зубчатых передач

Синтез зубчатых передач

ЗУБЧАТЫЙ МЕХАНИЗМ

Зубчатые передачи являются наиболее распространенными узлами современных машин и в значительной степени определяют их качество и конкурентоспособ­ность. Они предназначены для передачи вращения и крутящего момента от одного вала механизма к другому с заданным отношением угловых скоростей. Наиболь­шее распространение в современном машиностроении получили эвольвентные зуб­чатые передачи. Они отличаются компактностью, высоким КПД, постоянством пе­редаточного отношения, надежностью работы, высокой долговечностью и просто­той обслуживания.

Многообразие машин, механизмов и систем приводов сопровождается и многообразием структурных схем зубчатых передач. Они создаются на основе различных сочетаний простых передач с наружным и внутренним зацеплением. Комбинируя число простых передач и связи между их звеньями, можно полу­чать сложные многопоточные и многоступенчатые передачи с необходимыми свойствами. Вследствие компактности и малой массы, получили распространение многопоточные планетарные передачи, а также более сложные приводы, постро­енные на основе их сочетаний с другими передачами и устройствами.

Геометрия прямозубой передачи, состоящей из колес, нарезанных в станочном зацеплении с производящей рейкой, полностью определяется следующими пара­метрами: z₁, z₂, m, a, h_a * , с * , ρ * , x₁, х₂, где z₁, z₂ – числа зубьев колес;
m – модуль зубьев; a, h_a * , с * , ρ * – параметры исходного производящего контура, соответственно равные (ГОСТ 13755-81): угол профиля α = 20°; коэффициент высоты головки зуба h_a * = 1, коэффициент радиального зазора с * = 0,25, коэффициент радиуса переход­ной кривой ρ = 0,384; х₁, x₂ – коэффициент смещения исходного производящего контура, которые выбираются в зависимости от конкретных условий работы зубчатой передачи и требований, предъявляемых к ней.

Основные размеры зубчатого колеса определяемые из рассмотрения станоч­ного зацепления нарезаемого колеса с производящей рейкой (рис. 4.1) следующие.

Делительный окружной шаг зубьев

Радиус делительной окружности r определим из равенства 2πr = рz:

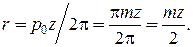(4.2)

Рис. 4.1. Станочное зацепление

Радиус основной окружности r_b.

Линия станочного зацепления касается основной окружности нарезаемого колеса. Из треугольника ОМП(рис. 4.1)

(4.3)

Радиус окружности впадин r_f.

Поверхность впадин нарезаемого колеса формируется вершиной зуба произ­водящей рейки, следовательно, радиус окружности впадин будет (рис. 4.1)

где или

(4.4)

Для колёс, нарезаемых без смещения (х=0),

Делительная толщина зуба S.

Толщина зуба S по делительной окружности равна ширине впадины рейки по начальной прямой (рис. 4.2).

Таким образом, .(4.5)

У колес, нарезаемых без смещения, .

Рис. 4.2. К определению делительной толщины зуба

Толщина зуба на произвольной окружности.

Из рис. 4.3 можно записать

,

где j – половина угловой толщины зуба по делительной окружности; j_у – половина угловой толщины зуба на окружности радиуса r_y.

Рис. 4.3. Определение толщины зуба на произвольной окружности

Выразив угловую толщину зуба через окружную, получим

или

. (4.6)

Угол профиля зуба на окружности радиуса r_y можно определить из треугольника ОМК:

. (4.7)

Дата добавления: 2015-03-31 ; Просмотров: 839 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Зубча́тое колесо́ или шестерня́ [1] , зубчатка [2] — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Обычно термины зубчатое колесо, шестерня, зубчатка являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй, а ведомое — колесом [2] . Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось») [3] .

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то крутящий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

Содержание

Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

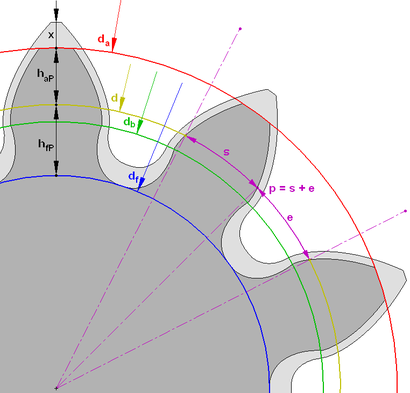
Параметры эвольвентного зубчатого колеса:

• m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

m = d z = p π <displaystyle mathbf >=<frac

<pi >>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 <displaystyle mathbf <<frac >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m <displaystyle mathbf >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 <displaystyle mathbf >> >

Продольная линия зуба [ править | править код ]

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на: