Потенциальная энергия упругой деформации формула

Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругой деформации. При этом точка приложения внешней силы перемещается, потенциальная энергия положения груза убывает на величину, которая численно равна работе, совершённой внешней силой. Таким образом, потенциальная энергия упругой деформации U равна работе внешней силы А. Найдём величину А (рис.2.28).

Внешняя сила P_t растёт от нуля до конечного значения Р. Соответственно и деформация ∆ℓ_t растёт от нуля до конечного значения ∆ℓ. Пусть некоторой растягивающей силе P₁ соответствует деформация ∆ℓ₁. Дадим силе бесконечно малое приращение dP₁, при этом деформация получит приращение d∆ℓ₁. Очевидно, работа внешней силы на этом перемещении

dA равна площади заштрихованной фигуры.

,

.

Теперь найдём работу внешней силы:

.

Итак, потенциальная энергия упругой деформации

. (2.36)

Если поделить U на объём образца Fℓ, получим удельную потенциальную энергию упругой деформации

. (2.37)

Потенциальная энергия деформации накапливается в обратимой форме – в процессе разгрузки тела она освобождается, превращаясь снова в энергию внешних сил и совершая работу. Таким образом, упругое тело – это аккумулятор энергии.

Глава 3. Напряжённое и деформированное

СОСТОЯНИЕ В ТОЧКЕ. ТЕОРИИ ПРОЧНОСТИ

3.1. Компоненты напряжений. Виды напряжённых состояний

Центральное растяжение или сжатие бруса является самым простым видом деформации тела, когда напряжение во всех его точках одинаково (однородное напряжённое состояние). В произвольным образом нагруженном теле (рис.3.1,а) напряжение меняется от точки к точке и поэтому в произвольном сечении m-n этого тела напряжения распределены неравномерно. В этом случае при изучении распределения напряжений в окрестности произвольной точки K рассматриваемого сечения m-n мысленно вырезают бесконечно малый параллелепипед (рис.3.1,б). Ввиду его малости можно считать, что по граням напряжения распределены равномерно. На рис.3.1,в показаны напряжения, действующие по граням бесконечно малого параллелепипеда.

σ_х – нормальное напряжение, действующее по направлению оси x; положительное при растяжении, отрицательное при сжатии;

τ_ху – касательное напряжение, действующее по площадке с нормалью х (первый индекс) в направлении оси у (второй индекс); положительно, если стремится развернуть элемент по часовой стрелке (глядя со стороны положительного направления оси).

На рис.3.1,в нормальные напряжения σ_х, σ_у и σ_z положительные, касательные напряжения τ_ху 0. Под действием приложенных к нему напряжений элемент должен находиться в равновесии, следовательно, для него можно записать уравнения статики. Покажем напряжения, дающие момент относительно оси OZ (рис.3.2) и запишем соответствующее уравнение статики:

∑ M_oz = 0: ; (3.1)

Учитывая правило знаков, перепишем формулу (3.1)

Формула (3.2) выражает закон парности касательных напряжений: на любых взаимно перпендикулярных площадках касательные напряжения с одноимёнными индексами равны по величине и вращают элемент в противоположные стороны.

Таким образом, шесть независимых компонентов напряжений σ_х, σ_у, σ_z, τ_ху, τ_ух, τ_zx – характеризуют напряжённое состояние в точке.

Напряжённым состоянием в точке называется совокупность напряжений, действующих по всевозможным площадкам, проведённым через эту точку.

При повороте бесконечно малого параллелепипеда меняются компоненты напряжённого состояния. Всегда можно найти такое его положение, что по граням (площадкам) параллелепипеда будут действовать только нормальные напряжения. Такие площадки называются главными, а нормальные напряжения, по ним действующие, называются главными нормальными напряжениями (рис.3.3).

Это положение доказывается в теории упругости. Главные нормальные напряжения принято обозначать цифровыми индексами по следующему правилу: σ₁ > σ₂ > σ₃. Соблюдение этого правила важно с точки зрения расчёта на прочность. Например: три главных напряжения имеют значения 120 МПа, – 50МПа и – 30 МПа; их надо записать σ₁ = 120 МПа, σ₂ = – 30 МПа и σ₃ = – 50 МПа.

Напряжённое состояние в точке классифицируется на три вида: линейное (одноосное), плоское (двухосное) и объёмное (трёхосное) в зависимости от того, испытывает ли параллелепипед растяжение (сжатие) в одном, двух или трёх взаимно перпендикулярных направлениях (рис.3.4).

Любое упруго деформированное тело обладает потенциальной энергией, так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.

Растяжение будем производить очень медленно, чтобы силу 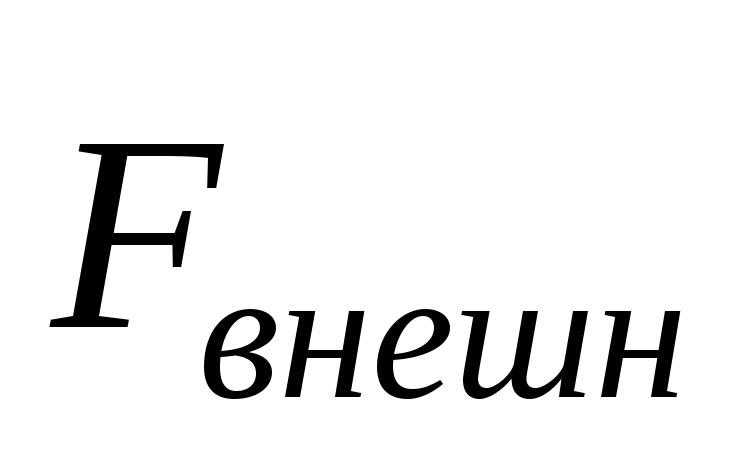, с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе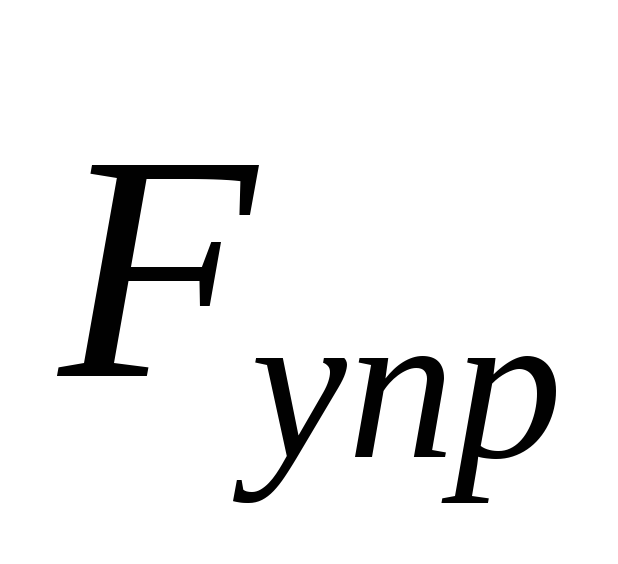. Тогда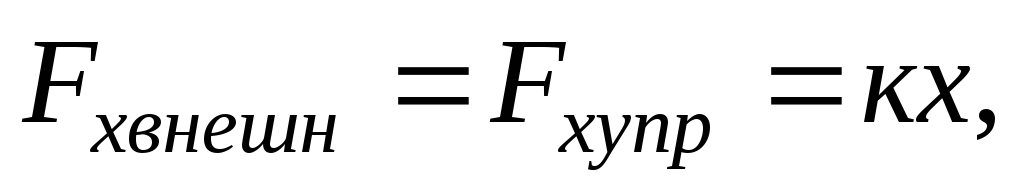гдек, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна

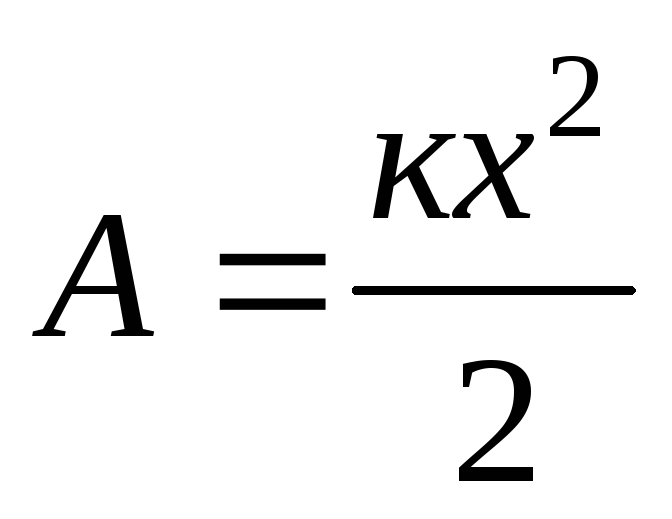(8.12)

Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид

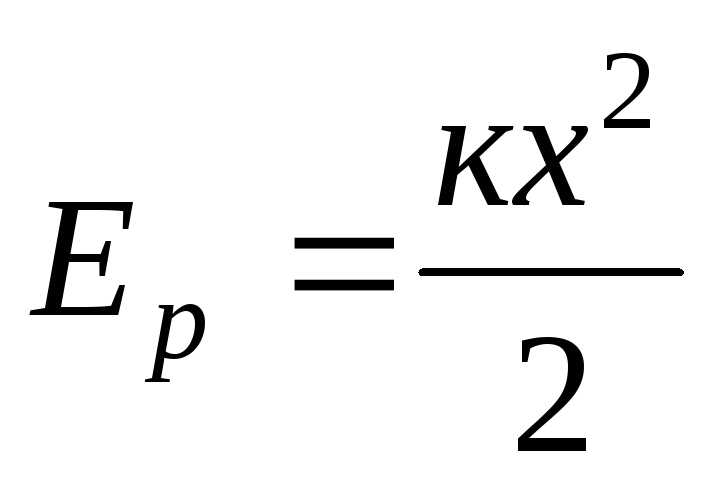, (8.13)

если считать, что потенциальная энергия недеформированной пружины равна нулю.

Потенциальная энергия упруго деформированного стержня равна

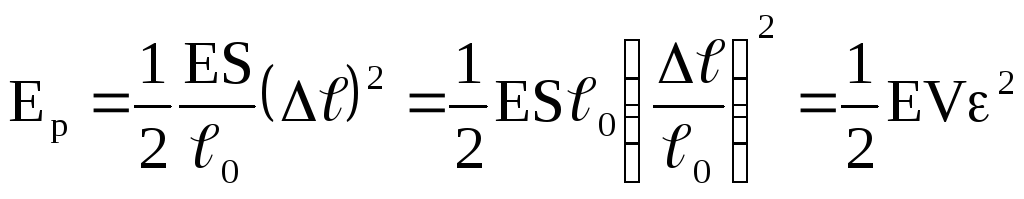, (8.14)

где 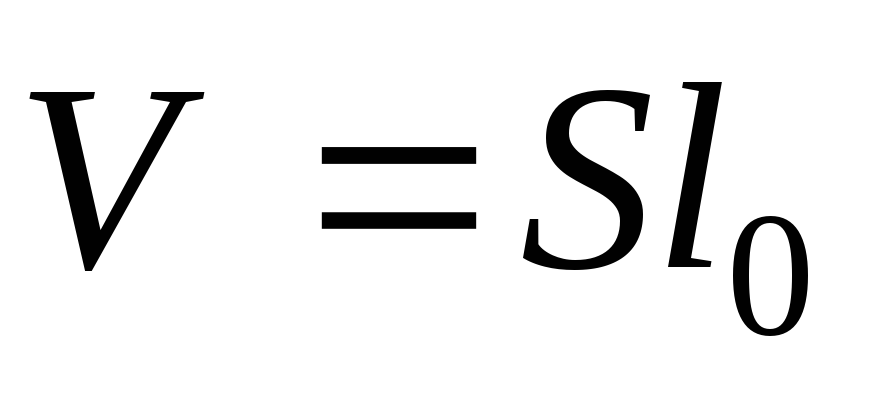– объем стержня.

Отношение энергии 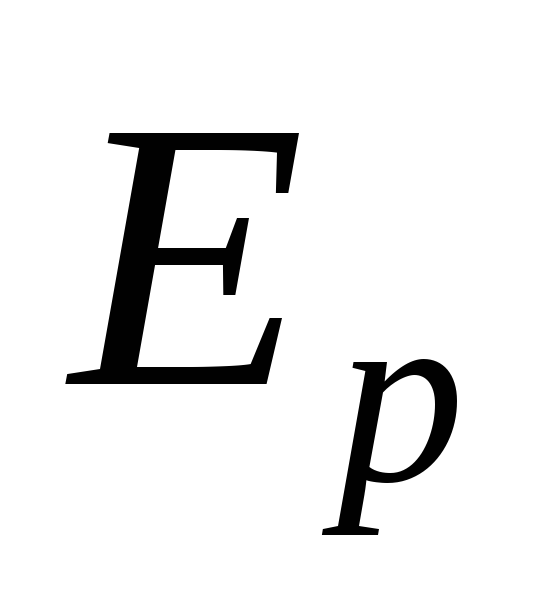к тому объему, в котором она заключена, называетсяплотностью энергии u. Тогда 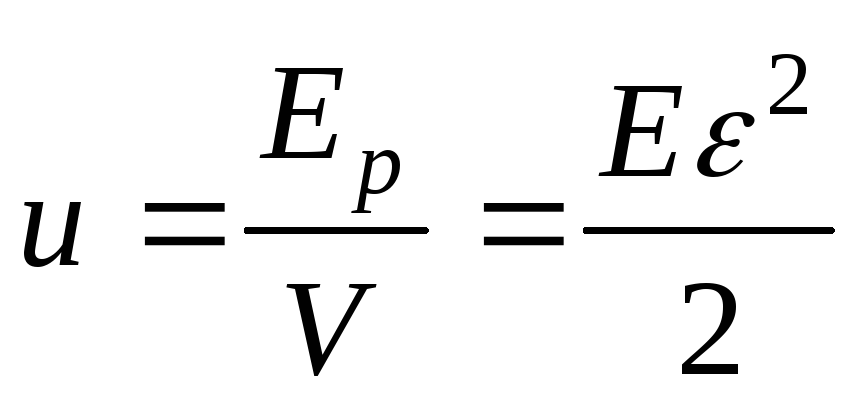– плотность энергии упругой деформации при растяжении (или сжатии).

Аналогично нетрудно получить, что плотность энергии деформации при сдвиге равна .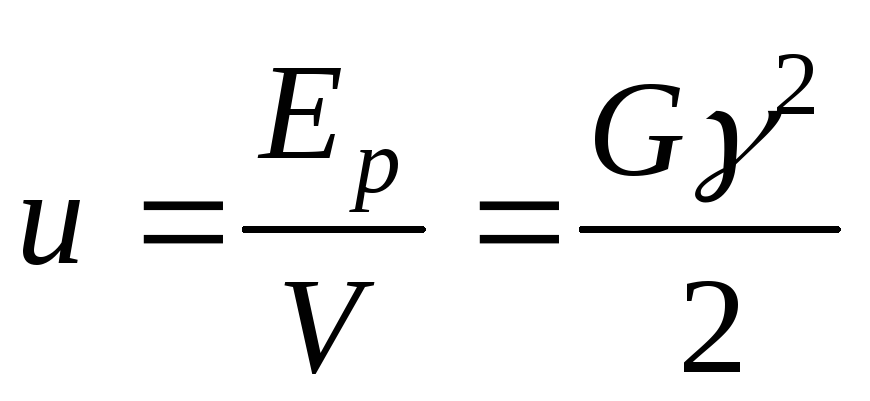

6. Кручение

Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, верхний конец ее закрепим, а к нижнему концу приложим закручивающие силы. Они создадут вращающий момент относительно продольной оси проволоки. При этом каждый радиус нижнего основания повернется вокруг продольной оси на угол . Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид

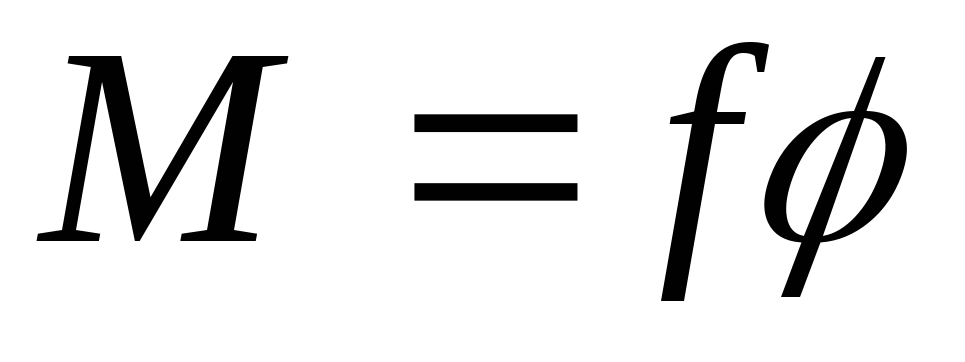_, (8.15)

где 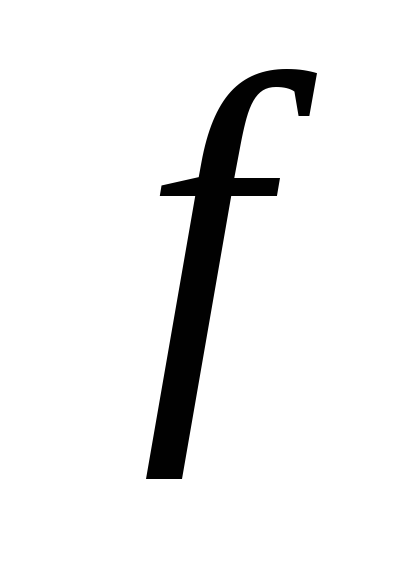– модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения.

Пусть имеется цилиндрическая трубка радиуса 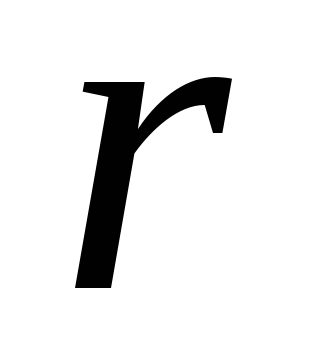. Причем толщина ееочень мала по сравнению с радиусом. Площадь сечения трубки равна 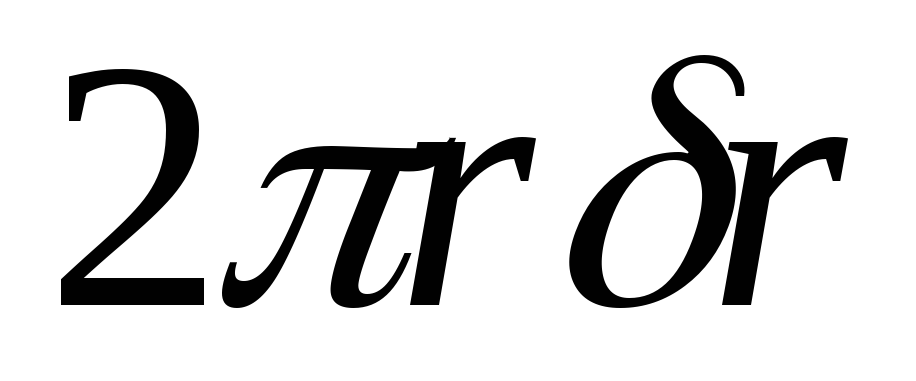. Обозначим черезкасательное напряжение в том же основании. Тогда момент сил, действующий на это основание, будет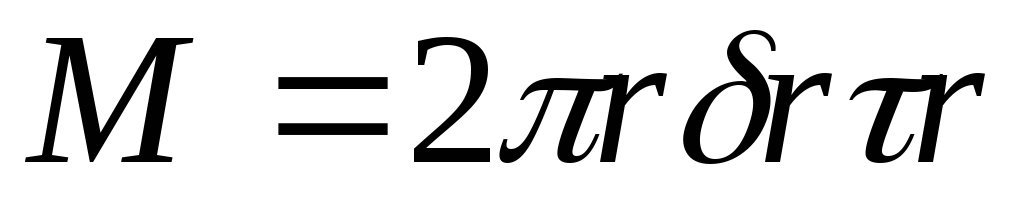. При закручивании совершается работа.

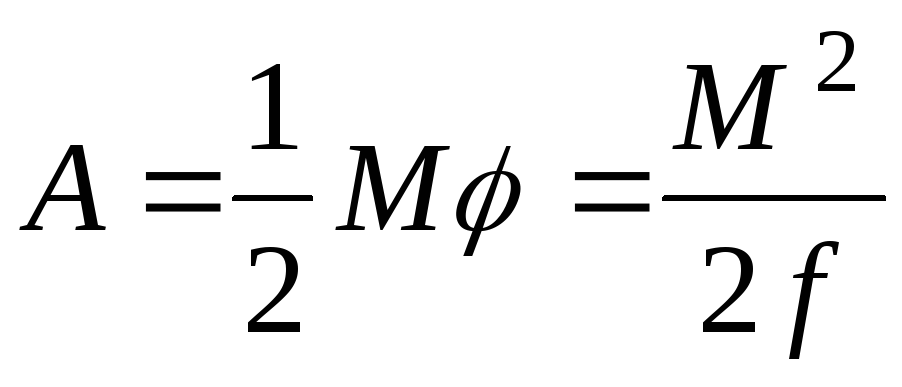Разделим ее на объем трубки 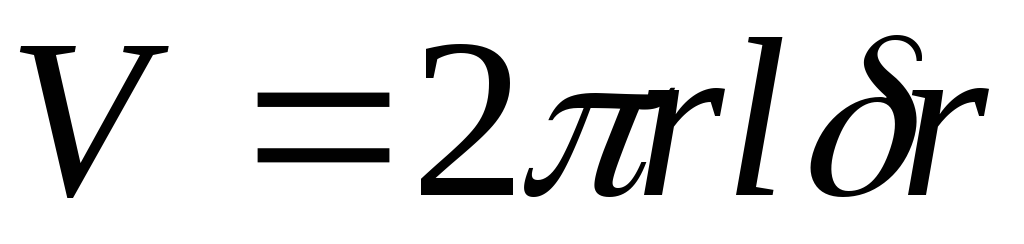. Найдем плотность упругой энергии при деформации кручения

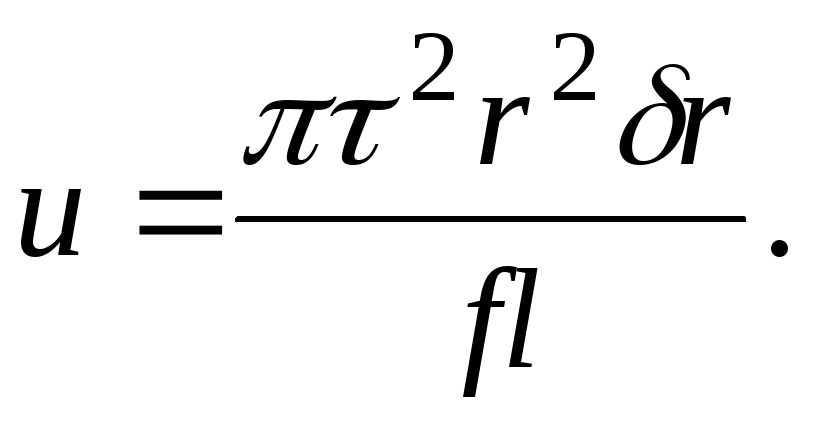(8.16)

Найдем эту же величину иначе.

Мысленно вырежем из трубки бесконечно короткую часть (рис.8.5).

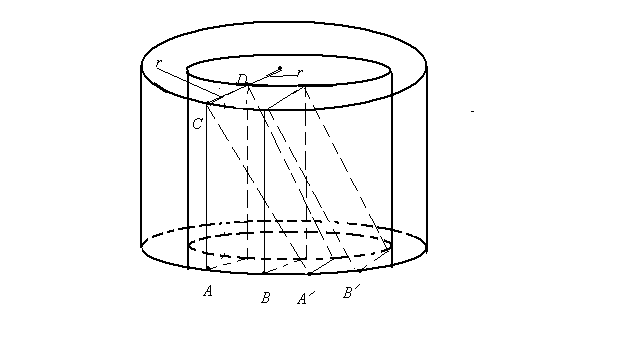
В результате кручения бесконечно малый элемент трубки ABDC перейдет в положение 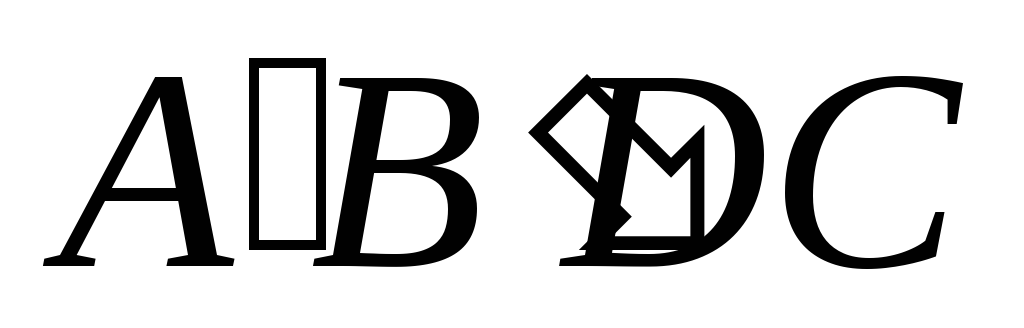. Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна

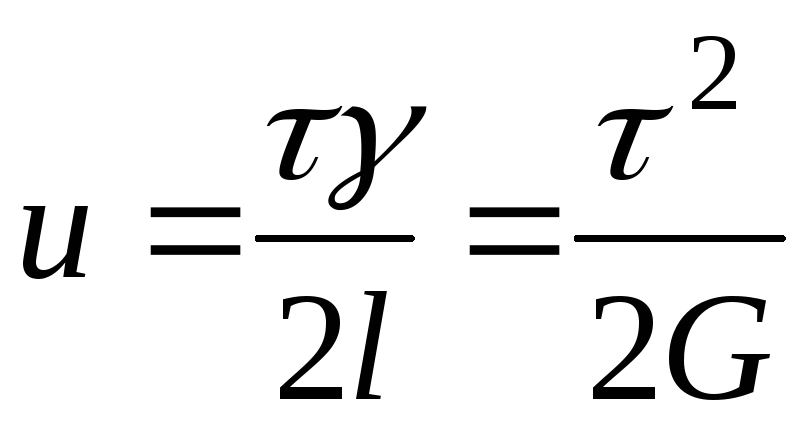(8.17)

Приравнивая его выражению (8.16), находим искомое соотношение

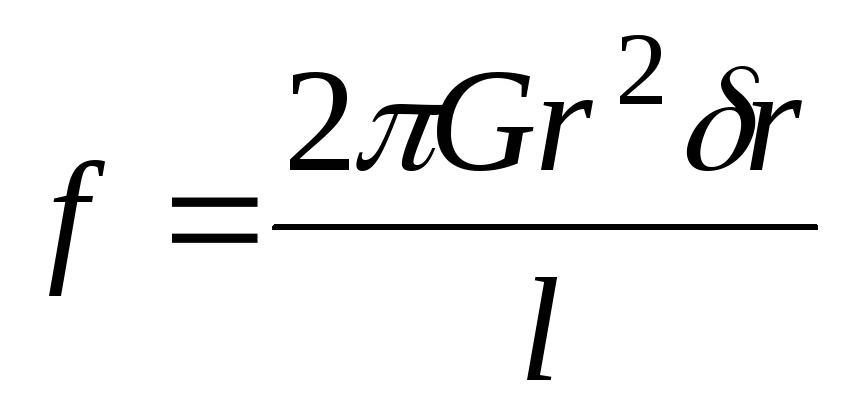(8.18)

Если стенка трубки имеет конечную толщину, то модуль найдется интегрированием последнего выражения по. Это дает 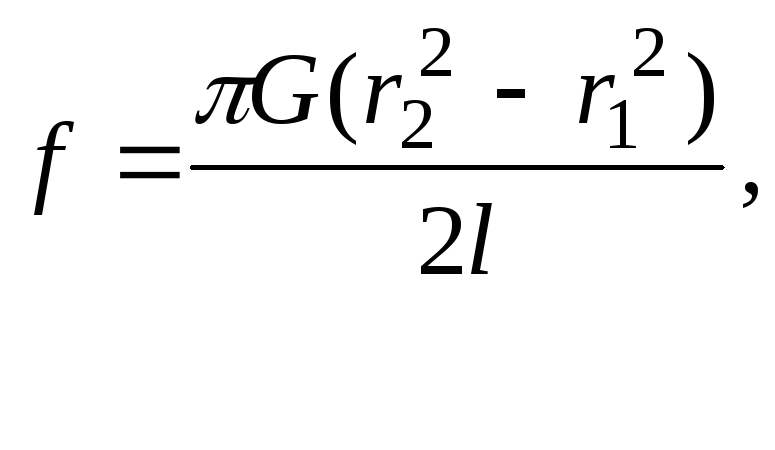где 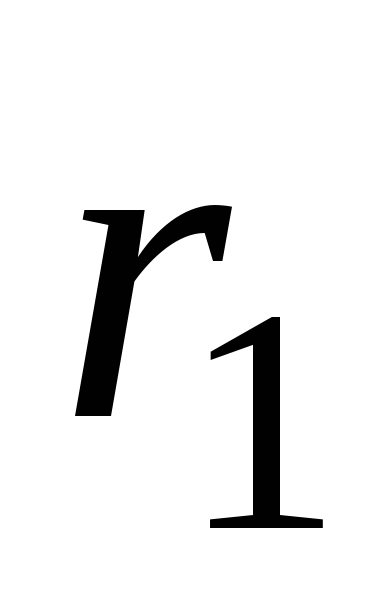– внутренний радиус трубки,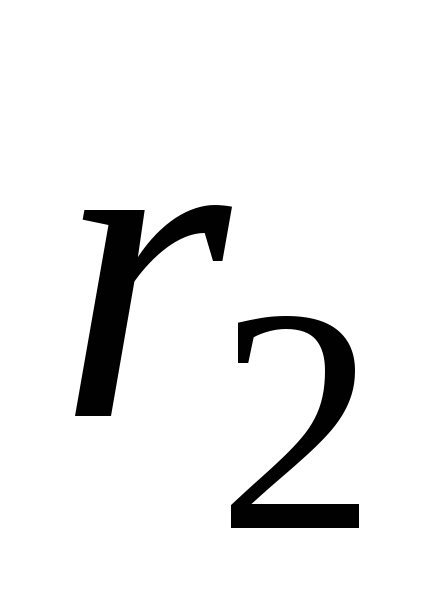– внешний радиус трубки.

Для сплошной проволоки радиуса 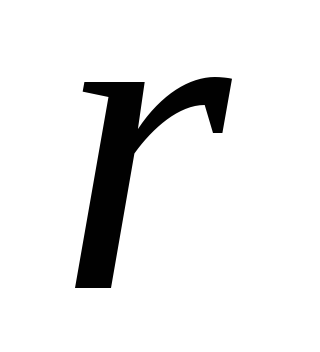_{модуль кручения .}

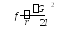Контрольные вопросы

Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.

Какова физическая сущность упругих сил?

Сформулируйте закон Гука? Когда он справедлив?

Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?

Что такое упругий гистерезис и упругое последействие?

Каков физический смысл модуля Юнга и модуля сдвига?

Что такое упругое последействие?

Выведите выражения для деформаций при всестороннем растяжении.

Что называется коэффициентом Пуассона?

Определите энергию деформированного тела.

Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.

Рис.3.13

Аналогично получим выражения и для двух других главных удлинений. В результате

(3.25)

Формулы (3.25) носят название обобщённого закона Гука для изотропного тела. Заметим, что сжимающие напряжения подставляют в эти формулы со знаком минус. Из формул (3.25) легко можно получить закон Гука для плоского напряжённого состояния. Например, для случая σ₂ = 0

(3.26)

Подчеркнём, что равенство нулю напряжения σ₂ не означает, что ε₂ также равно нулю. Например, при растяжении пластинки в её плоскости по второй формуле (3.26) можно определить уменьшение толщины пластинки.

Выражения (3.25) справедливы не только для главных деформаций, но и для относительных линейных деформаций по любым трём взаимно перпендикулярным направлениям, поскольку при малых деформациях влияние сдвига от действия касательных напряжений на линейную деформацию представляет собой величину второго порядка малости. Иными словами, индексы «1», «2» и «3» могут быть заменены на индексы х, у и z.

3.5.2. Относительная объёмная деформация

Установим связь между относительным изменением объёма элементарного параллелепипеда и главными напряжениями. До деформации размеры сторон были dx, dy и dz (рис.3.14,а). После деформации эти размеры стали dx + ∆dx, dy + ∆dy и dz + ∆dz (рис.3.14,б).

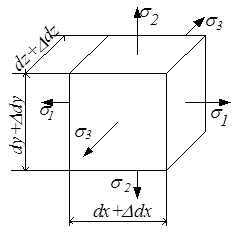
Начальный объём параллелепипеда V = dx∙dy∙dz. Объём после деформации V₁ = (dx + ∆dx)(dy + ∆dy)(dz + ∆dz).

Найдём абсолютное изменение объёма параллелепипеда:

. (а)

В скобках выражения (а) содержатся относительные удлинения

, , .

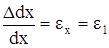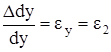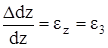Произведя в выражении (а) перемножение величин, стоящих в скобках, получим

Учитывая малость относительных деформаций, произведением их можно пренебречь. Тогда относительное изменение объёма

. (3.27)

Выразив главные удлинения через главные напряжения при помощи формул обобщённого закона Гука (3.25), получим:

. (3.28)

Формулу (3.28) перепишем в несколько ином виде, с учётом (3.22)

(3.29)

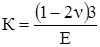. (3.31)

Величина К называется модулем объёмной деформации. Формула (3.30) представляет собой компактную, отличную от (3.25), формулу записи обобщённого закона Гука. Она удобна ещё и тем, что совпадает по структуре с законом Гука при линейном напряжённом состоянии (σ = Еε).

Из формулы (3.28) видно, что при деформации тела, материал которого имеет коэффициент Пуассона ν = 0,5 (например, резина или сталь в пластичном состоянии) объём тела не меняется. Материал ведёт себя как несжимаемая жидкость.

Из формулы (3.28) также следует, что коэффициент Пуассона не может быть больше 0,5. Действительно, при равномерном всестороннем сжатии (гидростатическом давлении) σ_ср = – р. И если материал будет иметь ν > 0,5, тело увеличит свой объём, что невозможно. Опыты подтверждают это положение: в природе не существует материала с коэффициентом Пуассона, большим 0,5.

Как отмечалось выше (см. п. 2.8), в процессе упругой деформации в теле накапливается потенциальная энергия, равная работе внешних сил. При осевом растяжении (линейном напряжённом состоянии) удельная потенциальная энергия (т.е. энергия, приходящаяся на единицу объёма) определяется по формуле (2.37)

.

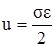В общем случае объёмного напряженного состояния

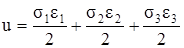. (3.32)

Подставив значения ε по формуле (3.25), получим

. (3.33)

Экспериментальные исследования показали, что прочность материала зависит не только от величины компонентов напряжений, но и от характера напряжённого состояния. Так, большинство твёрдых тел противостоит без разрушения действию очень большого всестороннего давления – при этом изменяется объём бесконечно малого элемента. И наоборот, те же тела разрушаются при сравнительно невысоких напряжениях, если эти напряжения изменяют форму элемента. Поэтому полную потенциальную энергию упругой деформации, определяемую по формуле (3.33), представляют в виде суммы двух составляющих:

где u – удельная потенциальная энергия изменения объёма, т.е. энергия, накапливаемая за счёт изменения объёма;

u_ф – удельная потенциальная энергия формоизменения, т.е. энергия, накапливаемая вследствие изменения формы элемента.

Для определения этих составляющих заданное напряжённое состояние представим в виде суммы двух напряжённых состояний (рис.3.15): изменяющего объём элементарного кубика (гидростатическое растяжение одинаковыми средними напряжениями) и изменяющего форму кубика.

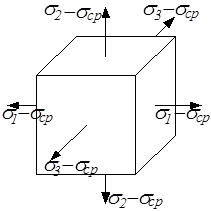
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 8814 — | 7171 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно