В чем измеряется эдс самоиндукции

Проводник с электрическим током имеет способность накапливать энергию в магнитном поле. Подобное явление называется индуктивностью. У обычного проводника, имеющего прямую форму, эта величина имеет небольшое значение, но если проводнику придать вид спирали и одинаковую направленность тока с соседними проводниками, то их поля будут взаимодействовать. При этом усилится индуктивность. Но есть факт того, что воздух значительно их ослабляет.

Человеческий мозг предположил следующее: поле должно протекать вокруг проводников не по воздуху, а по железу, сопротивляемость которого магнитному полю намного меньше. Такие катушки являются индуктивными.

Свойства

При подаче напряжения к индуктивной катушке, в ней происходит линейное нарастание тока, а при его снятии начинается его падение. Моментально остановить его протекание в катушке не представляется возможным, как, например, нельзя сразу остановить автомобиль, мчащийся на скорости. При попытке быстро остановить нарастание этого параметра, произойдёт удар напряжения, равный тому, что оно, при этом, может вызвать искровой разряд. Подобное явление получило название самоиндукция. На этом принципе основана работа катушки зажигания в автомобиле.

Коэффициент самоиндукции — это есть индуктивность. Иными словами: величина, которая характеризует связь между находящимся в проводнике электрическим током и магнитным полем, создаваемым при протекании. Эта мера представляет сумму потока индукции. Прямая зависимость её от конфигурации проводника и от проницаемости доказана.

При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока (Е =U), которое исчезает через некоторое время. Это противоположное напряжение называется ЭДС (электродвижущей силой самоиндукции). Параметр зависит от индуктивности катушки.

Как найти индуктивность

Формулы индуктивности будут выглядеть следующим образом:

• Ф = LI (магнитный поток в контуре);
• Е= LdI/dt (ЭДС самоиндукции).

ЭДС определяет энергию магнитного поля, от этой величины зависит противодействие системы при изменении тока. При этом ЭДС самоиндукции направлена противоположно последнему.

Перевод слова «индукция» с латинского языка (induct) — побуждение, наведение. Исходя из сказанного, понятно, что это величина, которая характеризует магнитные свойства электрической цепи. Ток проводящего контура создаёт в окружающем его пространстве магнитное поле. При этом, возникающий в контуре поток Ф, имеет прямую ему пропорциональность. Формально записывается это так: Ф=LI, где L — коэффициент пропорциональности или коэффициент самоиндукции контура. Его определяют размеры и формы контура, а также, магнитная проницаемость среды.

Энергия W магнитного поля тока I определяется по формуле: W =LI2/2. При проведении аналогии между электрическим и механическими явлениями, энергия сопоставима с кинетической энергией тела T=mv2/2, где m — масса, v — скорость. Тогда индуктивность подобна массе, а ток — скорости. Это наглядное сравнение помогает лучше понять суть. Эта интересная характеристика определяет инерционные свойства электрического тока.

На практике для увеличения её значения применяют катушки с сердечниками из ферромагнетиков, их свойства имеют зависимость от напряжённости магнитного поля и, следовательно, I. В основном это ферритовые пластины из электротехнической стали. Эффективность применения сердечников довольно значительна: индуктивность катушки возрастает в несколько раз. Помимо цилиндрических, распространены тороидальные варианты, они позволяют достичь большей индуктивности, из-за наличия замкнутого магнитного потока.

Индуктивность соленоида определённой длины, имеющего N витков и площадь поперечного сечения S в среде, имеющей проницаемость m равна:

где m0— магнитная проницаемость вакуума.

Определение индуктивности

Измерение индуктивности катушки можно провести в лабораторных условиях. За единицу индуктивности в системе СИ принимается 1 Генри — она измеряется в контуре с магнитным потоком в 1 Вб, сила тока при этом в контуре равна 1 Амперу. В системе Гаусса индуктивность равняется 1 Гн = 10⁹ см.

Для того, чтобы её определить, нужно измерить действующее значение переменного тока и его частоту, а также, напряжение на катушке и её активное сопротивление:

1. R —омическое сопротивление катушки.
2. F — частоту переменного тока.
3. U — напряжение.
4. I — силу тока.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

• сглаживание пульсаций и помех, накопление энергии;
• создание магнитных полей в различных устройствах;
• фильтры цепей обратной связи;
• создание колебательных контуров;
• трансформаторы (устройство из двух катушек, связанных индуктивно);
• силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
• ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
• применение катушек в качестве электромагнитов различных исполнительных механизмов;
• обмотки электромагнитных реле;
• индукционные печи;
• установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Урок 8. Физика 11 класс

Конспект урока "Самоиндукция. Индуктивность"

«Науку часто смешивают с знанием.

Это глубокое недоразумение.

Наука есть не только знание, но и сознание,

т.е. умение пользоваться знанием»

Явление электромагнитной индукции состоит в том, что в замкнутом контуре при изменении магнитного потока в нем возникает электрический ток, который называют индукционным.

Закон электромагнитной индукции гласит: среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограниченную контуром.

Знак «минус», в математической записи закона, учитывает правило Ленца, согласно которому электромагнитная индукция создает в контуре индукционный ток такого направления, что созданное им магнитное поле препятствует изменению магнитного потока, вызывающего этот ток.

Электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 году Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствии изменения внешнего магнитного поля. Оказалось, что изменяющийся электрический ток, проходящий в контуре, создает изменяющийся магнитный поток. Это явление было названо явлением самоиндукции.

Примечательно то, что и Генри и Фарадей работали над одной и той же проблемой. И пришли к одним и тем же выводам, касающихся как явления электромагнитной индукции, так и явления самоиндукции. При этом, Генри сделал свои открытия на несколько лет раньше, чем Майкл Фарадей. Но Генри был безответственно нетороплив при опубликовании результатов экспериментов, и Фарадей первым сообщил о своем успехе. Наконец, приоритет открытия электромагнитной индукции был отдан Фарадею, а Генри — открытие явления самоиндукции, которое он описал в той же самой статье, что и явление индукции,— в 1832 г.

Самоиндукция является важным частным случаем явления электромагнитной индукции. Если электрический ток в замкнутом проводящем контуре по каким-либо причинам изменяется, то изменяется и магнитное поле этого тока (т.е. индукция магнитного поля пропорциональна силе тока в контуре). Но при изменении индукции магнитного поля, создаваемого током, проходящим в контуре, изменяется и магнитный поток (т.е. магнитный поток будет пропорционален индукции магнитного поля). Следовательно, магнитный поток через поверхность, ограниченную контуром, пропорционален силе тока в контуре.

Коэффициент пропорциональности между магнитным потоком и силой тока Томсон (в последствии лорд Кельвин) в 1853 году предложил назвать «коэффициентом самоиндукции».

Коэффициент самоиндукции, который часто называют просто индуктивностью контура, обозначают L.

Индуктивность в СИ измеряют в Гн (генри).

Эта единица определяется на основании формулы

Индуктивность контура равна 1 Гн, если при силе постоянного тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой этот контур находится.

Например, если взять однослойный соленоид, то его индуктивность будет определяться по формуле

где — это число витков, приходящихся на единицу длины соленоида,

S — площадь поверхности, ограниченной витком,

l — длина соленоида,

m — магнитная проницаемость среды.

Из формулы для магнитного потока следует, что изменить его можно изменяя силу тока в контуре, или его индуктивность, или и то и другое одновременно.

Согласно закону электромагнитной индукции изменяющийся магнитный поток создает в контуре ЭДС. Возникновение ЭДС индукции в контуре, которое вызвано изменением магнитного поля тока, проходящего в этом же контуре, называют явлением самоиндукции, а появляющуюся ЭДС — электродвижущей силой самоиндукции или ЭДС самоиндукции.

Обозначается ЭДС самоиндукции греческой буквой x_Si. Измеряется ЭДС самоиндукции в В (вольт).

По закону электромагнитной индукции среднее значение ЭДС самоиндукции, возникающей в контуре прямо пропорциональна индуктивности контура и скорости изменения силы тока в контуре (при учете, что индуктивность контура остается постоянной).

Из этой формулы следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Используя это выражение, можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.

Поскольку контур замкнут, ЭДС самоиндукции создает в нем ток самоиндукции, силу которого определяют по закону Ома

где R — сопротивление контура.

Знак минус в формуле для ЭДС самоиндукции учитывает правило Ленца, согласно которому ток самоиндукции всегда направлен так, что он противодействует изменению тока, создаваемого источником. Если основной ток возрастает, то ток самоиндукции направлен против тока источника, если уменьшается, то направление тока источника и тока самоиндукции совпадают.

Как же пронаблюдать явление самоиндукции?

Для этого соберем электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока.

При замыкании цепи лампочка 2 начинает светиться практически сразу, а лампочка 1 с заметным опозданием. Происходит это из-за того, что при возрастании силы тока I₁, созданного источником, на участке, образованном катушкой и лампочкой 1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции направлен навстречу тока источника. В результате рост силы тока на этом участке цепи замедляется, и сила тока не сразу достигает своего максимального значения.

Явление самоиндукции можно также пронаблюдать и при размыкании цепи. Для этого соберем цепь, состоящую из катушки с большим количеством витков, намотанных на железном сердечнике, к зажимам которой параллельно подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки. В качестве источника тока возьмем источник с небольшим ЭДС.

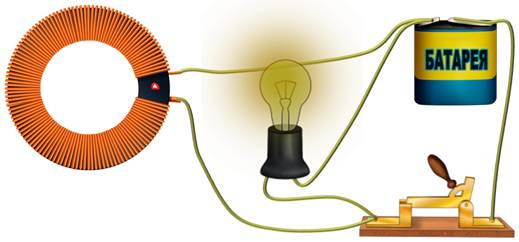
При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединенных катушки и лампочки. Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений.

Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает.

Почему это происходит?

Все дело в том, что при размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки.

Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.

Вообще, явление самоиндукции подобно явлению инерции в механике.

Известно, что автомобиль не может мгновенно приобрести определенное значение скорости, как не может и мгновенно остановиться, как бы велика не была тормозящая сила.

Точно так же, за счет самоиндукции при замыкании цепи, сила тока не сразу достигает своего максимального значения, а нарастает постепенно. При выключении источника, ток сразу не прекращается — самоиндукция будет поддерживать его некоторое время, даже не смотря на большое сопротивление цепи.

Задача: За промежуток времени 9,5 мс сила тока в катушке индуктивности равномерно возросла от 1,6 А до 2,4 А. При этом в катушке возникла ЭДС самоиндукции –14 В. Определите собственный магнитный поток в конце процесса нарастания тока.

– Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи, называют явлением самоиндукции.

– ЭДС самоиндукции равна произведению индуктивности контура и скорости изменения силы тока в нем.

– Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

– Единицей измерения индуктивности в СИ является Гн (генри).

– Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Если в контуре течёт переменный ток, то в этом контуре возникает ЭДС индукции, т.к. ток создаёт через контур переменный магнитный поток, величина которого изменяется в соответствии с изменениями тока. Возникающая ЭДС создаёт дополнительный ток в контуре. Это явление называется самоиндукцией, а дополнительные токи – экстратоками самоиндукции. Индукция магнитного поля пропорциональна току, следовательно, величина магнитного потока через контур также пропорциональна току: Φ = L∙I (3.12), где L – коэффициент самоиндукции или индуктивность контура, зависящая от формы и размеров, а также от свойств окружающей среды. Применяя к явлению индукции закон электромагнитной индукции Фарадея, получим:

ЭДС самоиндукции, возникающая в контуре при изменении тока в нём, прямо пропорциональна скорости этого тока. Индуктивность контура численно равна ЭДС самоиндукции, возникающей в нём при изменении тока на единицу за единицу времени.

Индуктивность можно сравнить с массой тела, т.к., чем больше индуктивность, тем труднее изменить силу тока в контуре. Индуктивность измеряется в генри – Н, Гн.

1 Гн – это индуктивность такого контура, в котором возникает ЭДС самоиндукции в 1 вольт при изменении тока в нём на 1 ампер за 1 секунду.

Рассмотрим электрическую цепь, состоящую из катушки индуктивности, источника питания и выключателя. Изменение тока через катушку индуктивности после включения в момент времени t ₁ будет выглядеть следующим образом:

Если теперь выключить ток, то ЭДС самоиндукции пытается сохранить его, т.е. препятствует его уменьшению.

При отключении выключателя в момент времени t ₂ ток и магнитный поток уменьшаются до 0. Изменение тока вызывает в катушке ЭДС самоиндукции e_L , которая препятствует уменьшению тока через контур, поэтому ток уменьшается не мгновенно, а по экспоненте, как показано на рисунке. Скорость изменения тока зависит от индуктивности контура и его активного сопротивления. Их отношение определяет постоянную времени:

τ – постоянная времени контура в секундах;

L – индуктивность контура (Гн);

R – сопротивление контура (Ом).

Во время разрыва контакта переключателя напряжение между его контактами

U + e_L , которое может во много раз превышать напряжение источника питания.

Поэтому между контактами переключателя может возникать электрическая дуга, ионизирующая воздух и позволяющая после размыкания контактов протекать току ещё некоторое время. Искрение или образование дуги разрушает контакты, поэтому в большинстве случаев механические контакты снабжаются пружинами для ускорения их размыкания.