От чего зависит амплитуда колебаний пружинного маятника

Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

T = 2 π m k <displaystyle T=2pi <sqrt <frac >>> .

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

m a = − k x ⟺ x ¨ + k m x = 0 <displaystyle ma=-kxiff <ddot >+<frac >x=0>

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

x ¨ + k m x = f ( x ) <displaystyle <ddot >+<frac >x=f(x)> , где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

x ¨ + c m x ˙ + k m x = f ( x ) <displaystyle <ddot >+<frac ><dot >+<frac >x=f(x)>

Механическими колебаниями называются движения, характеризующиеся определенной повторяемостью во времени.

Колебания называютсясвободными (илисобственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармоническими колебанияминазываютсяколебания, при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса).

Пружинный маятник – это колебательная система, состоящая из груза массой т, закрепленного на пружине, и совершающая гармонические колебания под действием упругой силы 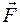, зависящей от величины линейной деформации x в соответствии с законом Гука: F_x = – kx, где k –жесткость пружины.

Согласно второму закону Ньютона уравнение движения маятника:

.

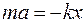Так как ускорение a является второй производной от смещения x ( 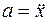), то

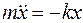или .

Если обозначить 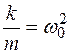, то получим дифференциальное уравнение свободных незатухающих гармонических колебаний пружинного маятника:

.

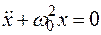Решением этого дифференциального уравнения является функция x(t):

,

где 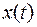– отклонение колеблющегося тела от положения равновесия в момент времени t;

А – амплитуда колебания, то есть максимальное отклонение колеблющегося тела от положения равновесия;

w –круговая (циклическая) частота;

(wt+j) – фаза колебания в момент времени t;

j –начальная фаза колебания.

Круговая частота ,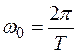

где Т – период колебаний, то есть время одного полного колебания.

Так как 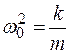, то период свободных незатухающих гармонических колебаний пружинного маятника .

Кинетическая энергия колебаний пружинного маятника:

.

Потенциальная энергияколебаний пружинного маятника:

.

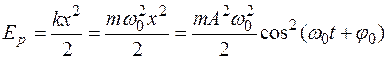Полная энергия колебаний пружинного маятника:

,

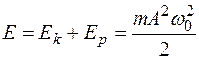откуда видно, что полная энергия свободных незатухающих гармонических колебаний пружинного маятника остается постоянной.

Свободные затухающие гармонические колебания пружинного маятника(рис. 6). Для пружинного маятника массой т, совершающего колебания под действием упругой силы 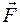(F_x = – kx)с учетомсилы сопротивления , пропорциональной скорости 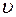движения груза ( 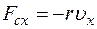), второй закон Ньютона имеет вид:

,

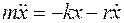где r – коэффициент сопротивления.

Обозначив 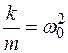и 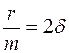( 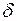– коэффициент затухания), получим дифференциальное уравнение свободных затухающих гармонических колебаний пружинного маятника:

.

Решением этого дифференциального уравнения в случае малых затуханий

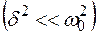является функция x(t):

,

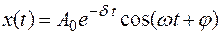где 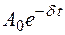– амплитудазатухающих колебаний в момент времени t;

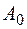– начальная амплитуда, т.е. амплитуда в момент времени t = 0,

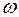– круговая (циклическая) частота: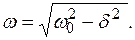

Периодзатухающих гармонических колебаний пружинного маятника:

.

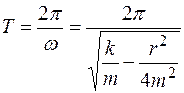Декремент затухания. Если A(t)и А(t+Т) – амплитуды двух последовательных колебаний (рис. 6), то отношение этих величин называетсядекрементом затухания .

Логарифм 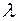называетсялогарифмическим декрементом затухания :

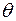Дата добавления: 2015-10-05 ; просмотров: 862 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Цель работы: изучение вынужденных колебаний пружинного маятника.

Колебательная система, выведенная из положения равновесия, самопроизвольно начинает колебаться с некоторой частотой, которая называется собственной. Если к такой системе приложить периодическую внешнюю силу, которая также изменяется с некоторой, в общем случае другой, частотой, то тогда система будет колебаться с частотой внешней силы, даже если эта частота не совпадает с частотой собственных колебаний пружины .

Когда мы раскачиваем качели, то имеем дело с их вынужденными колебаниями. При вынужденных колебаниях амплитуда колебаний, а следовательно, и энергия, передаваемая колебательной системе, зависят от того, насколько различаются частоты и , а также от величины сил сопротивления среды.

Рассмотрим пружинный маятник. На него действует сила упругости пружины F_упр = –kx, сила сопротивления среды F_сопр = –bv, которая обычно пропорциональна скорости движения и направлена в противоположную сторону. Наконец, на маятник действует внешняя, или вынуждающая, сила. Пусть внешняя сила синусоидальна и представляется в виде , где – циклическая частота изменения внешней силы. Тогда уравнение движения (2-ой закон Ньютона) с учетом сил сопротивления среды можно записать в виде:

Поскольку скорость является первой производной смещения, а ускорение – второй, то это уравнение является дифференциальным. Методы решения таких уравнений вам пока не известны, но из физических соображений можно догадаться, что тело будет колебаться, причем с частотой изменения вынуждающей силы. Таким образом, из физических соображений вынужденные колебания должны иметь вид:

где знак «-» перед начальной фазой колебания Ф говорит о том, что колебания запаздывают по сравнению с вынуждающей силой, так как отклик на воздействие всегда запаздывает по сравнению с самим воздействием.

Продифференцировав (2), можно вычислить скорость и ускорение частицы:

Если подставить эти выражения в уравнение движения (1), то можно найти амплитуду и начальную фазу колебания.

Величина называется коэффициентом затухания, она определяется силой сопротивления среды и пропорциональна ее.

Это решение уравнения движения (1) не описывает процесса установления вынужденных колебаний, оно описывает только установившиеся через некоторое время колебания. Амплитуда установившихся колебаний не зависит от начальных условий, например, от начального отклонения и от начальной скорости. Процесс установления колебаний зависит от начальных условий. Если начальная амплитуда слишком мала, то она постепенно увеличивается, если слишком велика, то уменьшается до величины, даваемой формулой (3).

Амплитуда вынужденных гармонических колебаний А сильно зависит от разницы между частотой вынуждающей силы и собственной частотой колебания системы. На рис. 1 показаны зависимости амплитуды А от частоты вынуждающей силы для трех значений постоянной затухания . Кривая 1 соответствует слабому затуханию, кривая 2 – более сильному, а кривая 3 – очень большой силе сопротивления среды, при которой в отсутствие внешней вынуждающей силы колебаний вообще не возникает.

Когда частота вынуждающей силы приближается к собственной частоте колебаний системы, амплитуда резко возрастает, если только затухание не слишком велико. При малом затухании рост амплитуды при оказывается очень сильным. Это явление называется резонансом. Собственная частота колебаний системы называется резонансной частотой. Если положить формально , то резонанс будет наблюдаться на частоте , а резонансный пик (амплитуда А) уходит в бесконечность, при этом энергия постоянно вводится в систему и не рассеивается.

В реальных системах никогда не обращается в нуль, поэтому резонансный пик имеет конечную величину; вершина пика не приходится точно на , хотя смещение частоты обычно невелико. Если же затухание велико, то пик выражен слабо или вовсе отсутствует (кривая 3 рис. 1).

Высота и ширина резонансного пика часто характеризуются параметром Q, который называется добротностью и определяется следующим образом . Чем меньше коэффициент затухания , тем больше добротность Q и тем выше резонансный пик. Значение Q характеризует также ширину резонансного пика: чем добротность выше, тем ширина уже.