В чем измеряют индуктивность

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике
(B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

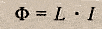
где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная — величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E₁ и с действующим значением напряжения U₁. На вторичной обмотке ЭДС E₂ и напряжение U₂.

Из законов Ома 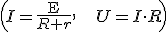следует, что напряжение на обмотке равно

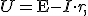(1)

где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r₁ делают очень малым, поэтому часто им можно пренебречь. Тогда

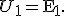
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e₁, как и ЭДС индукции e₂ в каждом витке первичной обмотки, т.е. e₁ = e₂. Следовательно, отношение ЭДС в первичной E₁ и вторичной E₂ обмотках равно отношению числа витков в них:

(2)

Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I₁/I₂ приблиз = w₁/w₂ = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.

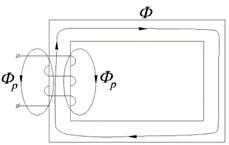
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

.

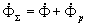(1.14)

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

.

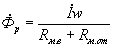Так как 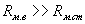, то .То есть поток рассеяния 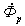, в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 8814 — | 7171 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Теория индуктивностей

Характеристики магнитного поля

Магнитное поле создается постоянными магнитами и проводниками, по которым протекает электрический ток. Для характеристики магнитного поля вводятся такие величины:
Напряженность магнитного поля, характеризующая интенсивностъ магнитного поля в данной точке пространства. Напряженность магнитного поля, создаваемого током, определяется его величиной и формой проводника. Напряженность магнитного поля, в а/м внутри катушки. у которой длина намного больше диаметра, может быть определена по формуле

где I — ток (в а); w— число витков, l — длина катушки (в м).
Магнитный поток — общее количество магнитных силовых линий, пронизывающих контур. Для вакуума и практически для воздуха магнитный поток в веберах – вб, определяется по формуле

где S — площадь контура в квадратных метрах.
Магнитная индукция — интенсивность результирующего магнитного поля в данном веществе измеряется в веберах на метр квадратный (вб/м2)

Магнитная проницаемость — величина, показывающая, во сколько раз магнитная индукция в данном веществе больше или меньше на пряжеиности внешнего магнитного поля (ом*сек)/м

Магнитная проницаемость вакуума (магнитная постоянная) равна единице. Для воздуха μ приблизительно равна 1. У парамагнитных веществ (алюминий, платина) μ > 1, у диамагнитных (медь, висмут и др.) μ >> 1. В соответствии с приведенными выше формулами для любого вещества можем написать:

Кроме практической системы единиц, пользуются абсолютной электромагнитной системой единиц. Соотношение между единицами этих систем следующее:

1 = 12,56*10-3 Э (эрстед);
1 вб = 108 мкс (максвелл);
1 вб/м2 = 104 гс (гаусс).

Индуктивность и взаимоиндуктивность

Индуктивность (коэффициент самоиндукции) численно равна э. д. с. самоиндукции (eL), возникающей в проводнике (контуре) при равномерном изменении тока в нем на 1 а в 1 сек.

Индуктивность, измеряется в следующих единицах:
1 гн = 1000 мгн;
1 мгн = 1000 мкгн;
1 мкгн = 1000 см.

Рис. 1 Схема взаимосвязанных индуктивностей.

Коэффициент взаимоиндукции М численно равен э. д. с. взаимоиндукции, возникающей в одном контуре при равномерном изменении тока на 1 а в 1 сек. в другом контуре (рис. 1).

Коэффициент взаимоиндукции измеряется в тех же единицах, что и индуктивность. Связь через общий магнитный поток двух катушек индуктивностью L1 и L2 называется индуктивной связью, характеризуемой коэффициентом связи

Зная коэффициент связи, можно определить коэффициент рассеяния

Если катушки находятся на общем замкнутом ферромагнитном сердечнике достаточно большого сечения, то k приблизительно равно 1, а ϭ приблизительно равна .

Соединение индуктивностей

Общая индуктивность L нескольких последовательно или параллельно соединенных индуктивностей при отсутствии, а также при наличии индуктивной связи между ними определяется по формулам, приведенным в таблице №1.

Таблица № 1

Схема соединения	Общая индуктивность

В формулах отмеченных значком * верхний знак алгебраического сложения, используется при согласованном включении индуктивностей, а нижний знак алгебраического сложения, используется при встречном включении индуктивностей.

Катушки с малой индуктивностью

Однослойные катушки

применяются на частотах выше 1500 кГц. Намотка может быть сплошная и с принудительным шагом. Однослойные катушки с принудительным шагом отличаются высокой добротностью (Q = 150 — 400) и стабильностью. Они применяются в основном в контурах КВ и УКВ. Высокостабильные катушки, применяемые в контурах гетеродинов на КВ и УКВ, наматываются при незначительном натяжении проводом, нагретым до 80—120°.
Для катушек с индуктивностью выше 15 — 20 мкГн применяется сплошная однослойная намотка. Целесообразность перехода на сплошную намотку определяется диаметром катушки. В таблице № 2, приведены ориентировочные значения индуктивности, при которых целесообразен переход на сплошную намотку:

Таблица № 2

Диаметр каркаса (в мм.)

10

15

20

25

30

Предельная индуктивность (в мкГн)

30

50

100

200

500

Индуктивность простой однослойной катушки может быть рассчитана по формуле (1):

где L — индуктивность (в мкГн), D — диаметр катушки (в см), I — длина намотки (в см), w — число витков.

При намотке однослойной катушки индуктивности с принудительным шагом, общая индуктивность (в мкГн), рассчитывается по формуле (2):

где L — индуктивность катушки, найденная по формуле (1) т. е. без поправки на шаг намотки;
А и В — поправочные коэффициенты, определяемые по графикам рис. 2а и 2б;
D — диаметр (в см);
w — число витков катушки.

Рис. 2 Графики поправочных коэффициентов для расчета индуктивности однослойных катушек с принудительным шагом намотки
d — диаметр провода;
t – шаг намотки;

Многослойные катушки могут быть разделены на простые и сложные. Примерами простых намоток являются рядовая многослойная намотка и намотка внавал.

Несекцнонированные многослойные катушки с простыми намотками отличаются пониженной добротностью и стабильностью, большой собственной емкостью, требуют применения каркасов со щечками.

Широкое применение имеют сложные универсальные намотки. В радиолюбительской практике находит применение также сотовая намотка. Индуктивность многослойной катушки может быть рассчитана по формуле:

где L — индуктивность катушки (в мкГн), D — средний диаметр намотки (в см), l — длина намотки (в см), t — толщина катушки (в см), w — число витков.

Если задана индуктивность и нужно рассчитать число витков, то следует задаться величинами D, l и t и подсчитать необходимое число витков. После этого следует произвести проверку толщины катушки по формуле:

где t — толщина катушки (в см), l — длина намотки (в мм), w — число витков. d — диаметр провода с изоляцией (в мм), α — коэффициент неплотности намотки. Значения коэффициента неплотности α, для многослойной намотки, могут быть взяты из таблицы 4.

Таблица 4

Диаметр провода без изоляции в (мм)

Коэффициент неплотности α

0,08 — 0,11

1,3

0,15 — 0,25

1,25

0,35 — 0,41

1,2

0,51 — 0,93

1,1

Более 1,0

1,05

Для намотки «внавал» α надо увеличить на 10% — 15%. Если фактическая толщина катушки отличается от принятой в начале расчета более чем на 10%, то следует задаться другими размерами катушки и повторить расчет.

Секционированные катушки индуктивности — рисунок 3, характеризуются достаточно высокой добротностью, пониженной собственной емкостью, меньшим наружным диаметром и допускают в небольших пределах регулировку индуктивности путем смещения секций.

Рис. 3 Секционированная катушка индуктивности.

Они применяются как в качестве контурных в контурах длинных и средних волн, так и в качестве дросселей высокой частоты.
Каждая секция представляет собой обычную многослойную катушку с небольшим числом витков. Число секций n может быть от двух до восьми, иногда даже больше. Расчет секционированных катушек сводится к расчету индуктивности одной секции. Индуктивность секционированной катушки, состоящей из n секций,

где Lc — индуктивность секции, k — коэффициент связи между смежными секциями.
Коэффициент связи зависит от размеров секций и расстояния между ними. Эта зависимость изображена на графике — рисунок 4.

Рис. 4 График зависимости коэффициента связи от размеров секций и расстояния между ними.

Отношение b/Dср выбирается так, чтобы величина коэффициента связи была в пределах 0,25 — 0,4. Это получается при расстояниях b = 2l. Расчет каждой секции производится обычным способом.

Корзиночная катушка, изображена на рисунке 5. Это плоскоспиральная намотка на основание в виде круга с нечетным числом радиальных прорезей. Через каждый разрез провод переходит с одной стороны круглого основания на другую.

Рис. 5 Корзиночная катушка индуктивности.

Индуктивность такой катушки в мкГн определяется по формуле:

где w — число витков, D2 — внешний диаметр намотки (в см), D1 — внутренний диаметр намотки (в см), k — поправочный коэффициент для корзиночных катушек, определяемый из таблицы 5.

Таблица 5. Поправочный коэффициент k для корзиночных катушек.

k

Наилучшим соотношением для корзиночных катушек является D2 = 2D1

Торроидальные катушки индуктивности на немагнитном сердечнике — выполняются сплошной намоткой на кольцевом немагнитном сердечнике, со средним диаметром D , как правило, поперечное сечение кольца имеет форму окружности с диаметром d . Эскиз торроидальной катушки индуктивности на немагнитном сердечнике изображен на рисунке 6.

Рис. 6 Торроидальная катушка индуктивности на немагнитном сердечнике.

Индуктивность такой катушки в мкГн определяется по следующей формуле:

где D — средний диаметр торроидального сердечника (в см.), w — количество витков катушки, d — диаметр витка (в см.)

Собственная емкость катушек индуктивности

Собственная емкость изменяет параметры катушки, понижает добротность и стабильность настройки контуров. В диапазонных контурах эта емкость уменьшает коэффициент перекрытия диапазона.
Величина собственной емкости определяется типом намотки и размерами катушки. Наименьшая собственная емкость (несколько пф) у однослойных катушек, намотанных с принудительным шагом. Многослойные катушки обладают большей емкостью, величина которой зависит от способа намотки. Так, емкость катушек с универсальной намоткой составляет 5—25 пф, а с рядовой многослойной намоткой может быть выше 50 пф.

Катушки с большой индуктивностью

В катушках с большой индуктивностью применяются сердечники из ферромагнитных материалов. Индуктивность катушки с замкнутым стальным сердечником, измеряется в генри (гн) и рассчитывается по формуле:

Где μ – магнитная проницаемость материала, Sc – сечение сердечника в квадратных сантиметрах см2, ω – число витков катушки, lc– средняя длина магнитного пути в см. Схематическое изображение Ш – образного магнитного сердечника, приведено на рисунке 7.

Рис. 7 Ш – образный магнитный сердечник

Следует помнить, что магнитная проницаемость материала зависит от переменной составляющей индукции в сердечнике и от величины постоянного подмагничивания, а также от частоты. Ниже приводится методика расчета катушек индуктивности, работающих при малых значениях переменной составляющей индукции, например, дросселей сглаживающих фильтров для выпрямителей. Для катушек индуктивности, работающих без постоянного подмагничивания, число витков определяется по формуле:

Где L – индуктивность катушки в гн, lc — средняя длина магнитного пути в см, μн – начальная проницаемость магнитного материала, Sc – сечение сердечника в квадратных сантиметрах см2.

Для катушек индуктивности с постоянным подмагничиванием предварительно определяем ориентировочное значение действующей магнитной проницаемости, с учетом подмагничивания, по графикам для разных электротехнических сталей, приведенным на рис. 8, где I — ток подмагничивания, L — индуктивность.

Рис. 8 Графики для ориентировочного определения
действующей магнитной проницаемости при
постоянном подмагничивании

Ориентировочное число витков для катушек индуктивности с постоянным подмагничиванием определяем по формуле (*) :

Где μд – истинное значение магнитной проницаемости материала ферромагнитного сердечника. Истинное значение действующей магнитной проницаемости μд определяется по кривым рисунка 9.

Рис. 9 Графики для определения истинного значения
действующей магнитной проницаемости при
постоянном подмагничивании

Постоянное подмагничивание awo на 1 см длины магнитного пути для работы с графиками рисунка 4, можно определить по формуле:

где Io — ток подмагничивания в ма, lс — длина магнитного пути в см.
Далее определяется точное число витков катушки по приведенной выше формуле (*). Диаметр провода катушки в мм :

Где Io — ток подмагничивания в а.
Величина немагнитного зазора в сердечнике, изображенного на рисунке 1 высчитывается по формуле:

причем Z% определяется по кривым рисунка 10. Толщина немагнитной прокладки выбирается равной 0,5δз. Прокладки можно делать из любого листового изоляционного материала.

Рис. 10 Кривые для определения величины z%

Индуктивность — это коэффициент пропорциональности между электрическом током, проходящим в замкнутом контуре и магнитным потоком, образуемым этим током через поверхность, у которой контур является краем. Индуктивность обозначается символом L, принятым в честь Э.Ленца.

Ф = L I , отсюда
L = Ф / I = 1Вб / 1А = 1 Гн

Ф — величина магнитного потока, которая пронизывает контур с 1 витком;
I — величина тока;
L — индуктивность витка;
L — коэффициент пропорциональности между Ф и I.

Если катушка состоит из N витков, то полным потоком (или потокосцеплением) будет сумма магнитных потоков через все витки, тогда

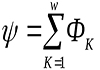
Индуктивность L зависит от размеров, формы проводника, количества витков и т.п., от магнитной проницаемости среды.

Единица измерения в системе СИ названа генри (Гн) в честь Дж.Генри. В Гауссовой системе и СГС, СГСМ системах индуктивность считают в сантиметрах 1 Гн = 1000000000 см, 1 см = 1 нГн. Для сантиметров используют название абгенри.в качестве единицы. В системе СГСЭ единицу индуктивности называют статгенри, либо оставляют без названия.

1 статгенри приблизительно равен 8,987552 х 10 в 11 степени генри.
1 Гн = 1000 Миллигенри
1 Гн = 1000000 Микрогенри
1 Гн = 0,001 Килогенри
1 Гн = 0,000001 Мегагенри

Рассчитать индуктивность и осуществить быстрый перевод единиц измерения можно с помощью онлайн калькулятора.

«>